liuyujie0136's Website

Logo

A website for self learning, collecting and sharing.

Contact Me

分子群体遗传笔记

By Evan from 微信公众号“AI写代码的DNA” and 知乎
资料来源：Molecular Population Genetics 1st Edition: by Matthew W. Hahn
仅供个人学习参考，仅改变个别错漏之处和排版格式，版权为原作者所有

（一）绪论

https://zhuanlan.zhihu.com/p/360236713

一、什么是分子群体遗传学

分子群体遗传是生物领域最具有魅力的一个研究方向，融合了分子生物学和基因组学的先进技术和群体遗传学的理论与实践。在很多顶尖学术期刊上和各种学术会议上你都能够看到分子群体遗传的影子。

分子群体遗传学不同于遗传学的另外两个主要分支：经典群体遗传学和定量遗传学。经典群体遗传和定量遗传学主要关注对进化过程和对未来的进化预测。研究自然选择、遗传漂变、突变、迁徙等因素对基因频率和表型频率的研究。

而分子群体遗传学是研究“历史”的一个遗传学分支，它关注于是过去哪种进化驱动力导致了目前的遗传状况，通过对遗传分子数据的分析去了解过去，而不在于对未来的预测。这是因为这种特性，分子群体遗传学也被称为“达尔文的侦探”。

分子群体遗传主要关注于三个方面的问题：

随着基因组测序技术的进步，如金钱和时间成本的降低，分子群体遗传研究的上述三个方面的问题正在快速融合：要想了解对某个基因的选择，我们必须比较自然选择在整个基因组水平的作用，要想了解选择在基因和基因组水平的作用，我们必须了解自然选择作用方式和作用效果的历史背景。

进化始于一个个体、一个染色体上的一个突变。分子群体遗传要研究自然种群中进化过程，这就需要通过研究群体中部分个体的DNA序列来弄清驱动整个群体进化的驱动力。这也是分子群体遗传常用的研究方法。通过基因位点的变异来推测突变、重组、自然选择以及群体数量在进化中的作用。

二、进化过程的模型

1、群体数量模型

遗传漂变是由于群体数量有限而造成的基因频率的随机变化。在一个群体中，有些染色体会传递给下一代，而有些不会。

Wright-Fisher (W-F) 模型是研究遗传漂变的经典模型。该模型假设群体数量为N，个体为二倍体，可以随机交配，子代与亲代没有世代重叠。某些一年生的植物或昆虫能够满足没有世代重叠，不过对脊椎动物，很难满足这个假设。但一般情况下，对假设没有那么严格的要求。

W-F模型的研究表明，在没有选择突变、没有选择压力的情况下，群体中平均等位基因的频率维持不变，基因频率的方差和群体数量有关系，群体数量越大，方差越小。虽然说总群体的等位基因频率维持不变，但是对于某个小群体，可能会出现该等位基因的丢失（基因频率 = 0）或者固定（基因频率 = 1）。这也就导致了该群体中基因变异性下降，同时群体中杂合子的数量也下降（2pq，当p = q = 0.5时，杂合子数量最多）。只有遗传漂变的情况下，杂合子下降速度为1/(2N)每代，也就是群体数量越大，杂合子下降速度越慢，对于一个小群体而言，遗传漂变会使群体子杂合子很快消失，而对于大群体，这是一个相当漫长的过程。

另一个模型是Moran模型，它不要求世代不能重叠，因而比W-F模型更实际一些。但严格意义上说，Moran模型只适用于单倍体。和W-F模型一样，Moran模型也显示在只有遗传漂变的情况下，平均等位基因的频率保持不变。但是，基因频率的方差却大了一倍，而杂合子在群体中下降的速度也快了1倍。

在实际使用中，由于W-F模型更加直观，所以使用也更加广泛。

2、有效群体数量 (Effective population size)

在W-F模型中，假设群体数量为N，这N个个体都有均等的几率留下后代。但实际中，并不是这样的，由于选择压力的存在，会有小于N个个体留下后代。这里就涉及到一个有效群体数量 (Ne)，它和实际的群体数量（“真”群体数量）不同，通常小于实际群体数量。更广义地讲，Ne并不是指个体数量，而是由W-F模型推定出来的，一个群体中，不同的基因组区域可能有不同的Ne。

关于Ne的概念确实是一个很抽象而且经常被误用的概念，有各种不同的定义方法。“有效”这个词的使用也通常会造成一些误解，与其说是“有效”，不如说“和W-F模型等效”。

3、突变模型

因为突变有不同的形式，因而突变模型也有很多。不过这里我们强调的突变并不是生殖细胞中一个变异的出现过程，而是以一种定量的方式去描述一个若干代之前的突变怎样变成了现在的一个基因多样性位点，以及不同的突变速率怎样导致了不同数量的多样性位点。

在分子群体遗传中，常用到的是随机突变模型，假设所有的突变都是随机的。实际上，突变并不是那么随机，比如碱基转换比颠换更多，染色体不同区域的突变差异也很大，如突变率在CpG位点要比普通位点大10倍。当然，“随机”在进化上是说，一个突变的发生并不会因为其是有利突变还是有害突变而改变突变概率。由于突变概率非常低，通常每个碱基每代只有在10e-8到10e-9之间的突变概率，所以描述随机突变通常用Poisson模型。

在早期人们研究变异的时候，DNA测序还没能广泛使用，人们只能使用蛋白凝胶电泳的方法来判断是否存在变异，这也就导致了很多同义突变没能检测到。通过这种技术研究突变的模型称之为“无限等位基因模型”。所以这里的“等位基因”实际上是指不同的单倍体型，它可能包含很多个或者很多次的突变。而现在我们所说的等位基因通常是单个碱基变异。由于”无限等位基因“模型忽略掉了很多变异信息，所以在现代分子群体遗传学中很少使用。

4、重组模型

和突变一样，重组的发生同样是小概率事件，可以用Poisson模型。重组在染色体上的发生并不是随机的，在染色体上存在很多“重组热点”，也就是很多重组事件发生的聚集区。当然，即便没有很明显的重组热点，染色体上重组的发生差异性也很大。重组的发生并不会改变群体中的基因频率，而单倍体型的频率会因此发生变化。

5、自然选择模型

一个新的突变通常会带来三种效应：有利、有害和中性。

通常用s表示一个新突变的选择系数，也就是带有一个该突变基因和没有该突变基因个体的适应性差异。如果s > 0，表示有利突变；s < 0，表示有害突变；s = 0，表示中性突变。

对一个基因或位点的自然选择通常有3中：负选择 (negative selection)，正选择 (postitive selection)，和平衡选择 (balancing selection)。

6、迁徙模型

种群不是固定在一个地方不变的，各个种群之间也会有迁徙。

迁徙率 (m)，是指在一个群体中从其他群体中迁入个体的比例。这里有两个假设，首先，迁入个体是其他群体中（源群体）的一个随机样本，也就是该迁入群体的基因频率和源群体的基因频率应该是一致的。第二，源群体和接受迁入群体的群体的数量不能因为迁入而改变。

下面是几种常用的迁徙模型：

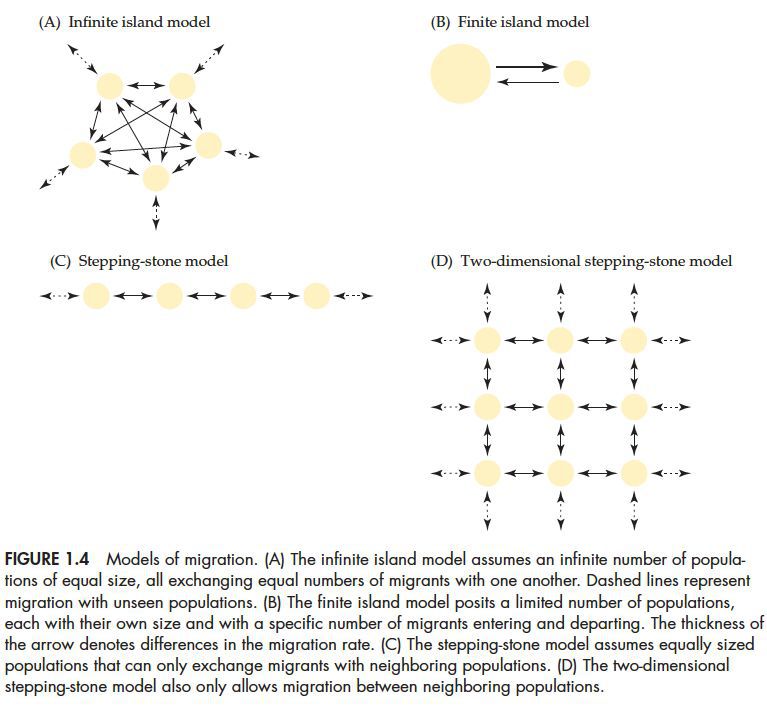
7、交配模型

最常使用的Hardy-Weinberg模型，它的假设是没有选择、没有突变、没有迁徙、没有遗传漂变、随机交配。

另外在实际中还有很对非随机交配情况，比如正相配交配和负相配交配。正相配交配是指具有相同形状的个体交配的几率更大（如身高高的更倾向于和身高高的个体交配）；负相配交配是指两种相反形状的个体交配的几率更大（如身高高的倾向于和身高矮的个体交配）。

正相配交配会显著增加群体内纯合子数量。一个极端的情况是近亲交配，会出现更多的纯合子。近亲交配系数F表示在基因组中由于近亲交配而造成同一来源的等位基因所占的比例。F从0到1，F越大表示亲代近亲交配越严重。

（二）分子进化理论

https://zhuanlan.zhihu.com/p/360239291

一、中性理论

很少有关于分子变异模式的解释，直到60年代后期，才有Motoo Kimura和Jack King& Thamas Jukes提出一个叫做“分子进化的中性理论”。到80年代，Kimura进一步解释了中性理论:

绝大多数变异并不是达尔文的自然选择造成的，而是中性或者近乎中性地在群体中被随机固定下来。不同物种间分子水平的差异，如蛋白质的多态性，也是近乎中性的，而多态性的维持主要是靠随机突变的产生以及突变的固定或消亡。

这一中性理论强调了两点：

  1. 物种间分子水平的差异主要是由于两个适应性差不多（中性）的等位基因的替换；
  2. 物种内多态性基因的适应性差异很小，近乎中性，多态性的维持靠“突变-遗传漂变”平衡。

所以，中性理论认为种间差异和种内差异的本质是一样的，都是近乎中性的等位基因在群体中受到遗传漂变的作用而产生的随机固定和丢失。

中性理论能够很好的解释基因中不同位点或者基因组中不同基因的进化速度的不同。中性理论并没否定负选择，实际上中性理论认为负选择而不是正选择是决定不同分子进化速度的关键因素。Kimura提到了一个公式：

u = vf

其中u是中性突变，v是总突变，f是中性突变在总突变中所占的比例。在一个基因或者基因组中，总突变速度是一定的，但f是一个限制因素，决定了各个位点不同的中性突变速度。f越大，限制作用越小，会有更多的中性突变，进化速度越快。比如，在氨基酸密码子中，能够简并4个碱基的密码子位点比能够简并2个碱基的密码子位点的限制性要弱很多，因而f要大，所以能够简并4个碱基的密码子进化速度更快。通常我们会认为能够简并4碱基的位点的f=1，也就是该位点的全部突变均为中性突变。同样地，对与基因也是如此，如果某个基因具有很重要的功能，突变可能会受到严格的负选择，那么该基因f会很小，相对会有更少的中性突变。

中性理论的另一个用途是能够很好的解释不同种群或者物种间核酸多态性水平的差异。如果在物种内一个位点的等位基因都是中性的，那么它的多态性水平仅仅受到中性突变和遗传漂变的影响。一个大的种群受遗传漂变的影响更小，而突变更多，因而大种群多态性要更高，反之，小种群中很多突变受到遗传漂变影响很大，要么固定（基因频率=1）要么丢失（基因频率=0），所以小种群多态性要小。

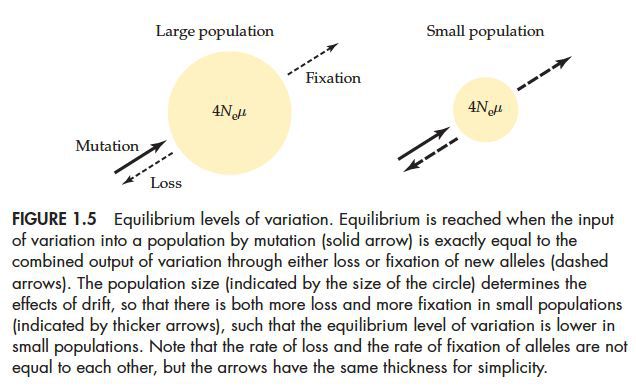
当然，中性理论也有很多局限性。对于基因组水平来说，大部分突变都发生在非编码区或者非功能区，都是中性的，中性理论能够很好的适用；但是对于发生在编码区或者功能区的突变来说，中性理论并不十分适合，很多因素影响到突变-遗传漂变的平衡。

二、关于中性理论的误解和误用

“中性”并不意味着没有选择。“中性”最早源于定量遗传学中，研究人员在说明突变和遗传漂变对表型进化的作用时，将“选择中性”混用为“没有选择”。

另一个容易弄混的地方是“中性突变”和“中性位点”。实际上只有中性突变，而不能说中性位点。对于位点，只能说位点没有受到选择的作用。关于中性突变和中性位点还有一下常见的错误理解：

  1. 认为只有未被限制的位点才有中性突变。实际上所有的位点都会有中性突变，只是中性突变多少的差异，受限制位点的中性突变少。
  2. 认为不受限制的位点也不会受到选择的影响。实际上不受选择的位点通常会和受选择位点有关联，也就是连锁不平衡，造成不受选择位点表现出“非中性”。
  3. 认为受到限制的基因或者位点总是“非中性的”。实际上一个中性进化的位点并不意味着没有选择，可能会有负向选择，但不会有其他形式的选择（正向选择、平衡选择等）。

三、其他分子进化模型

除了上述中性理论之外，还有其他一些关于分子进化的理论，但是其中很多都认为多态性和突变不是中性的。有三种典型的代表，其一是有害突变模型理论，认为所有的突变都是有害的，群体中的基因多态性主要是靠“突变-选择平衡”维持，而且多态性主要表现为过多的低频变异；第二个是有利突变理论，即突变都是有利的，群体中的基因多态性主要表现为突变固定过程中形成的等位基因，而且主要表现为过多的高频变异；第三个是平衡突变理论，群体中的基因多态性主要表现为中等频率的变异。这三种理论都存在很大的缺陷。

还有另外两种理论涉及基因关联性在选择中的作用，这两种理论能够很好的解释当前的观测数据情况。第一个是背景选择模型 (background selection model)，认为群体中的负向选择在剔除有害变异的同时，也会影响该变异附近的一些位点的多态性，造成附近位点多态性降低。这一理论没有否定大多数突变是中性的，这和有害突变模型理论是不同的。另一种是“搭便车”模型 (hitchhiking model)，认为有利的变异在迅速的固定过程中，会降低其附近位点的多态性，同样的，这一理论也没有否定大多数突变是中性突变。几乎可以肯定地说，这两种理论做描述的现象在生物群体中是同时存在的，只是我们还不能确定在不同基因组和不同物种之间，哪一种现象更为普遍。

最后，还有一个理论值得提一下，就是“近乎中性理论” (nearly neutral theory of molecular evolution)，它是对中性理论的补充，认为大多数突变是轻度有害（或者轻度有利的），用来解释氨基酸替换率的问题。

（三）实验设计及测序

https://zhuanlan.zhihu.com/p/360240631

要想研究进化过程，需要从一个群体中随机抽取一定量的个体进行测序。那么需要多少样本量？怎样做到随机？如何得到精确的序列数据？这都是在实验设计中需要仔细考虑的问题。

一、群体采样

分子群体遗传中经常用的样本量在10-50个染色体组（或者5-25个二倍体个体）。当然不同的研究目的，样本量的需求也不一样，比如如果我们只关注多态性位点数量，那么很少的样本量就够了，但是如果我们关注群体中的基因频率，那么需要的样本量会超过50个。

样本的采集也要尽量避免有遗传关系的个体，如直系或旁系关系的个体等。同时我们的采样还要来自一个单一个群体，也就是群体中的个体都可以自由交配。目前很多遗传数据分析方法都是基于单一群体的假设，所以从10个群体中每个抽取1个个体和从1个群体中抽取10个个体会有很大的差异。

二、DNA测序

根据不同的研究目的，确定不同的测序策略，比如哪些位点需要测序，是测一个位点还是多个位点，或者是全基因组测序。

测序方法：

  1. Sanger法：略
  2. 二代测序：能够高通量便宜快速的获得全基因组数据。二代测序需要参考基因组进行后期比对。二代测序有两个缺点，一是读长短，二是错误率高。当然随着技术的改进，二代测序的读长也在增加，错误率也在降低。

二代测序是同时进行数百万的片段序列测定，这些片段是随机被打断和选择的，这也就造成了各个位点的测序深度不同。有些位点被测过好多次，有些位点几乎没有被测到，造成整个染色体的测序质量差异很大，而且我们不能从测序样本中得到基因型。

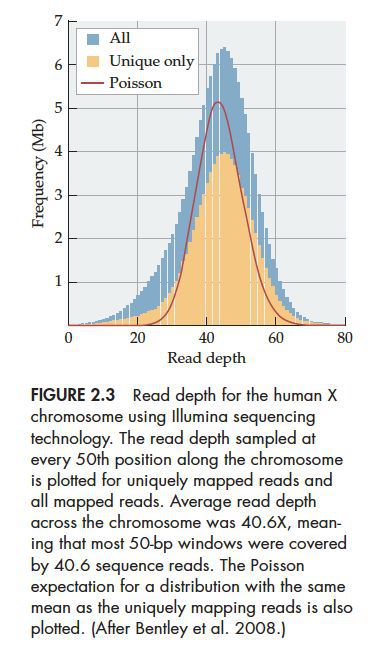
在实际中，有很多因素影响测序深度，比如模版序列的GC含量、DNA提取方法等。

短阅读片段的影响

二代测序的读长通常在35-600个碱基，分为单端测序 (single-end) 和双端测序 (paired-end)。双端测序就是来自同一条DNA的两个等长的测序片段从两端分别测序。双端测序能够发现拷贝数变异以及其他基因组的结构变异。测序完之后就是要把测序片段和参考基因组比对，常用的软件有BWA, Bowtie, SOAP和Stampy。

通过二代测序可以很可靠地发现测序样本和参考基因组的差异，来判断一个位点是不同类型的纯合子还是杂合子。如下图，黑框标出的是和参考基因组不同的纯合子型，其他字母为测序错误：

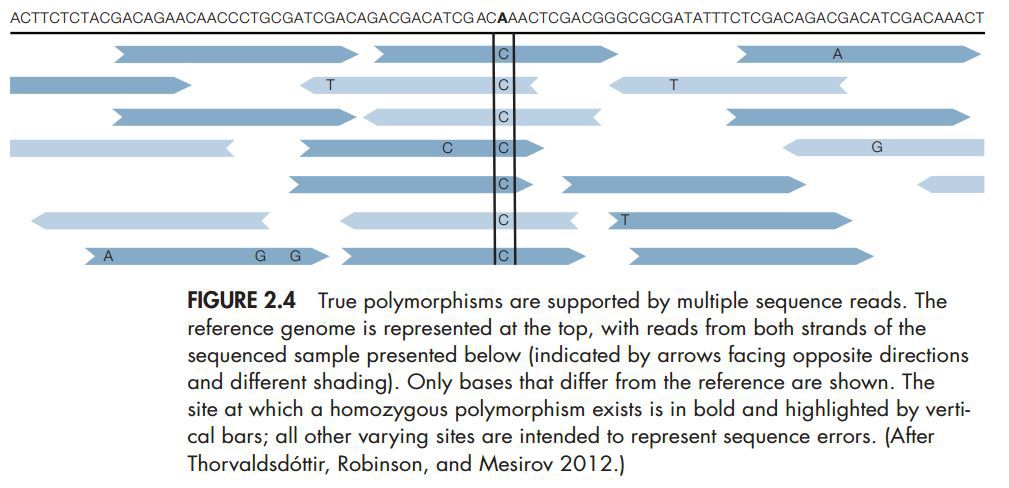
二代测序非常依靠参考基因组。参考基因组的来源有很多不同的方式，有些是单系自交来源的个体，有的是杂交个体等等。不管哪种来源，都要求样本能够提供足够高质量的DNA。所有的参考基因组都是在数据库中以单倍体形式呈现的，也就是参考基因组的多态性位点也有整合成一种状态。所以我们实际上使用的参考基因组也仅仅是一种单倍体样本，如果我们自己测序样本有比较大的变异（我们样本序列的插入或者参考基因组序列的删除），就无法比对到参考基因组上，造成整个序列测序深度偏倚很大。有时候一个测序读长可以比对到基因组的很多地方，这个时候就引入了一个比对质量评分 (mapping quality score) 的指标对每一个测序读长进行评价。一个读长能够在参考基因组中比对的地方越多，它的评分就越低。对于读长较短的测序而言，基因组的重复序列给基因组比对带来了极大的困难。

高错误率的影响

第二代测序的出错率要比Sanger测序高，虽然正在降低出错率，但每个碱基仍有0.3%的错误率。所以在只有一个读长覆盖的基因区域的序列，有很大可能会出现错误。不过测序错误也有一定的规律可寻，比如在每个阅读片段末端出现错误的概率要比起始端大。

同样的，为了评价每一个碱基的质量，引入了碱基质量评分 (base quality score)，表示出现碱基错误的概率。还有另一个综合性的评分 (consensus quality score)，它通常会考虑碱基质量评分指标、比对质量评分指标以及附近的碱基质量评分。在二代测序中通常使用SAMtools和GATK工具来判断SNP位点。

针对二代测序的不同实验设计

从上面的分析中可以看出，测序深度越高，越能够得到准确的DNA序列。那么到底需要多大测序深度？

这个问题要根据具体情况分析，比如测序样本的杂合子多少、测序群体和参考基因组的遗传距离、基因组中重复序列的多少等。可以通过Lander-Waterman模型来估计所需测序深度。一般而言，对于一个重复序列很少的自交系种群，10X的单端Illumina测序深度就足够了；对于人类个体而言，则需要30X双端测序。

为了获得准确的基因型，通常测序深度会很高（下图A），所以当有很多个个体需要测序的时候就会带来很大的工作量和花费。很多研究会使用测序深度较低的全基因组测序，虽然它不能保证每个个体的基因型都能被准确的测出，会错失掉很多低频等位基因，但是确实能够很快的发现大量的多态性位点（下图B）。还有一些研究使用部分基因组的高深度测序来代替全基因组测序，可以用来研究感兴趣的基因组区域变异情况。比如使用探针对外显子序列进行测序（下图C）。还有一些研究使用DNA限制位点测序 (restriction-associated DNA sequencing, RAD)，对特异性内切酶位点区域进行测序。通常在一个基因组中，只有数百到数千个位点可以进行切（下图D）。最后一种常用的方法是Pool-seq，就是将很多个个体放在一起测序，这种方法不能够得到某个个体的基因型，但是能够很精确的得到群体中基因频率（下图E）。Pool-seq测序是根据阅读片段来获得基因频率的，所以对于一个测序来说，有足够多的染色体远比测序深度要重要，也就是样本量要大。使用Pool-seq还可以用来检测基因组中的转移元件和拷贝数变异。

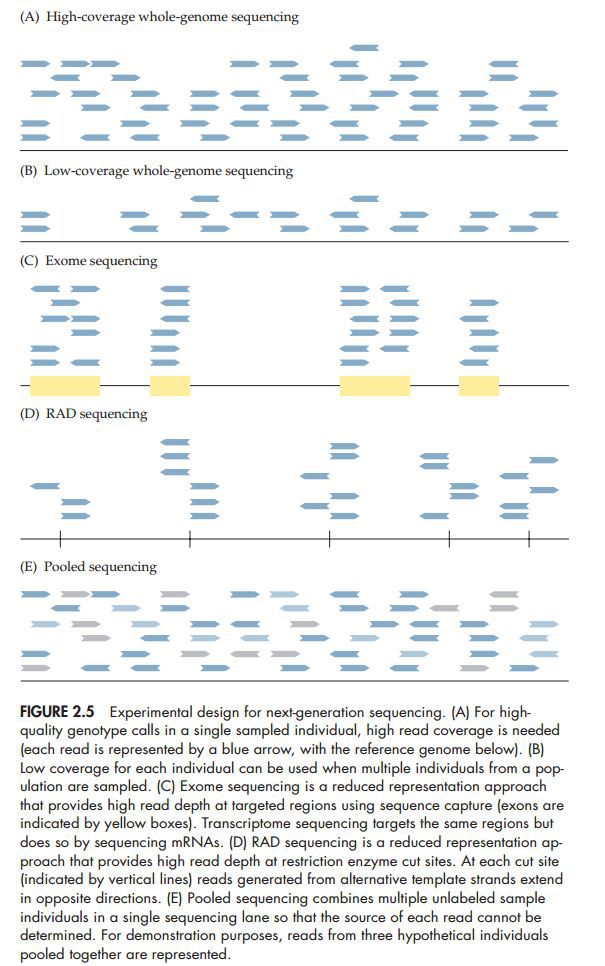
三、基因型

由阴性错误导致的基因型错判或者偏倚远比阳性错误造成的问题要大。如果参考基因组的碱基正好是祖系状态，那么阴性错误会严重低估等位基因频率。这也是为什么在数据处理中，宁愿将不可靠的碱基判定为缺失数据也不会轻易将其判定为阴性。

（四）变异的描述

https://zhuanlan.zhihu.com/p/360241563

针对不同类型的变异，有不同的统计量来描述变异。

在分子遗传学中常用到统计量θ(=4Neμ)来描述在没有选择的（仅有变异-遗传漂变平衡）的情况下常染色体的变异数量。有很多数学方法可以计算得到θ，比如极大似然估计和贝叶斯方法等。但是这些方法对数据量有限制，不能将整个基因组数据一起分析，同时它们对缺失数据的处理也存在问题。

一、在无限位点模型下SNP位点多样性估计θ

表示一个位点的杂合性，通常用下面公式计算：

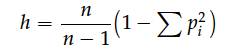
其中，n表示样本数量，π表示一个位点不同等位基因的频率。而如果我们要计算整个染色体或者序列片段的多样性，可以通过下面的计算公式完成：

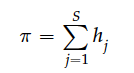
其中S是所有多态性位点的数量，h即第一个公式中的每一个位点的杂合性。对于满足Wright-Fisher平衡二倍体群体而言，π的期望值E(π) = θ。举例下图

如计算该片段的多态性，我们可以应用第一个公式分别计算每一个位点的杂合性（0.5，0.667，0.5，0.667和0.5），然后将其相加即 π = 3.33

还有另外一种计算形式：

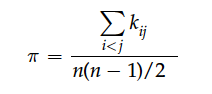
其中Kij是群体中序列两两比较时碱基不同位点的数量，n是样本数量。利用该公式计算的 π = 3.33，和第一种方法一样。但是如果序列的数量很多，第一种方法要比第二种方法简便一些。

不过当序列中有插入或者缺失时，两种方法的计算结果却不一样。比如下面一个例子：

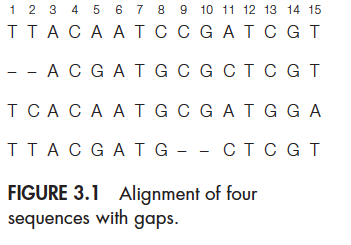
用第一种方法得到 π = 3.49，第二种方法得到 π = 2.83（排除了1，2，9，10这四个缺失位点），在第一种计算方法中使用了全部15个位点，第二种方法中，只有11个位点。所以当基因组中有很多缺失位点时，第一种计算方法要比第二种方法更好！

关于 π 的方差，在没有基因重组的情况下，可以用下面的公式表示：

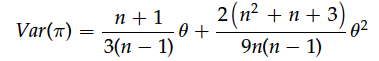
可以看出 π 的变异性与很多因素有关，即便样本量足够大，方差也不会为0。

另一种描述序列多样性的方法来自Watterson，公式如下：

其中S表示多态性位点的数量。这也就是著名的Watterson’s theta (θw)。

二、等位基因频谱

前面我们用π和θ来描述序列多样性，等位基因频谱同样可以描述。假设有如下图（A）一个基因序列，10条染色体，9个分离位点。针对每一个分离位点，如果我们不知道哪一个碱基是祖系状态，哪一个是后天得到的，那么这个时候 我们可以用Minor allele frequency(MAF)来描述，也就是“少数等位基因”频率。MAF的范围在1/n - 0.5之间，用条形图表示出来就是下图（B）。它也被称为Site frequency spectrum(SFS)。因为不能确定祖系状态，只能在“少数等位基因”，因而也被称为folded spectrum。

如果我们通过其他物种的基因组推测出了每一个位点的祖系状态，这个时候就可以用Derived allele frequency(DAF)来表示位点变异情况，DAF的范围在1/n - (n-1)/n之间，相对应的，也被称为unfolded spectrum，如下图。

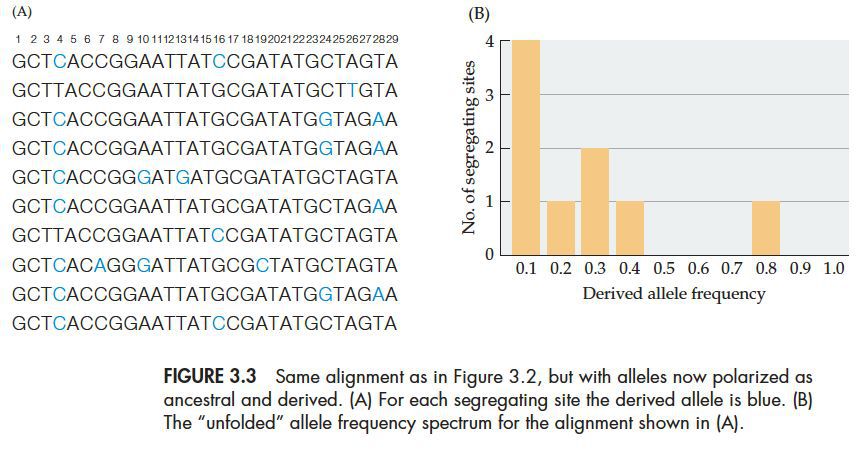
在基因组数据分析中，我们在不知道祖系状态的情况下，通常将MAF<0.05的位点舍弃，因为这可能是测序错误或者有害突变，并不一定代表基因的多态性。但是这也有可能包含了DAF>0.95的位点，也就是会丢失掉很多进化上很重要的位点。

如果我们知道了位点的祖系状态，那么还可以使用Fay and Wu’s θ来描述位点多样性。

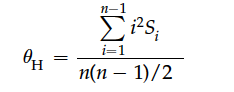
其中，Si表示有i个染色体含有S个derived位点。如计算上图中的θ可以是：

([1^2 * 4] + [2^2 * 1] + [3^2 * 2] + [4^2 * 1] + [8^2 * 1])/45 = 2.36

三、有限位点模型中序列多样性的测量

之前不管是π还是θ，都是假设一个位点只有两种状态，即不存在一个位点存在多碱基突变的情况。这对一些物种（比如人）是没有问题的，因为群体中的三碱基突变很少，几乎没有四碱基突变。但是对于有些生物却不同，突变位点比分离位点要多，按照分离位点估计会造成对位点多样性的低估。其中对θ的影响要比对π的影响大的多。

Tajima（1996）在假设没有测序错误（测序错误会造成对位点多样性的高估）的前提下，使用Jukes-Cantor对θ的计算方法进行了校正，将多碱基突变的情况也考虑在多样性的计算公式中。校正之后的值比校正之前略有增大，这也就暗示着校正之前因为多碱基突变的情况存在，导致了对位点多样性的低估。

四、核苷酸多样性的解释

在假设没有选择的情况下，按照中性理论，一个群体中的核苷酸多样性应该是：

E(π) = θ = 4Neμ

也就是一个位点的多样性水平和这个群体的有效群体数量以及中性突变率成线性关系。但是实际上我们观察到的很多物种的多样性和有效群体数量仅存在很弱的相关性，这也就是变异悖论。很多物种的有效群体数量会相差好几个数量级，但是它们的核苷酸多样性差异很小。相反的，人们却观察到重组率和变异水平成正相关关系！这是按照中性理论所没有预想到的。不过按照比如“背景选择”模型和“搭便车”模型，是可以预测出基因重组率增加会提高群体核苷酸多样性的。“背景选择”理论认为一个群体中的有害突变的比例越少，该群体的核苷酸多样性就会越多；“搭便车”理论认为随着重组率的增加，位点关联效应会降低，从而对该群体的核苷酸多样性的影响也降低，使得核苷酸多样性接近于中性理论的估计。

理论上θ = 4Neμ，但实际中很多统计量，π, θ(W), θ(H), η1, or ξ1并不等于4Neμ。不过通过上面的分析可以看出我们可以通过核苷酸多样性来反求Ne，这也就提供了估计Ne的一种方法。Ne的大小和实际种群数量并不是一回事，Ne只是一个在遗传中常使用到的“虚构”的一个量。虽然Ne经常用到，但是这并不意味着实际种群数量不重要。相反，实际种群数量对进入群体中突变的数量影响很大，对种群的进化也有着很重要的影响。

五、多样性的其他描述

  1. 微卫星变异
  2. 单倍体变异

（五）基因重组

https://zhuanlan.zhihu.com/p/360242228

连锁不平衡的衡量（LD）

连锁不平衡是一个非常拗口的词。我们先来看看什么是连锁平衡。如果两个位点的出现完全没有相关性，出现在一起的概率是随机的，那么它们就是连锁平衡。

比如有如下一个例子：

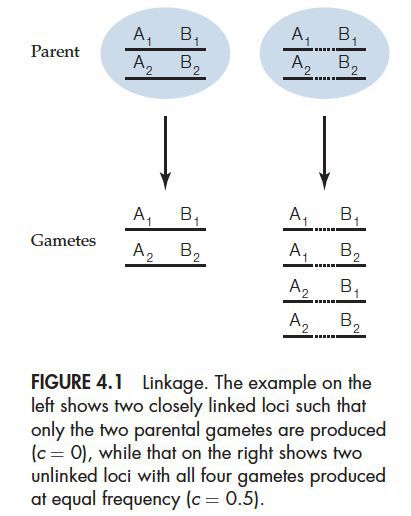
如果两个位点是紧密相连的，也就是子代中只有和亲代一样的单倍体型（A1B1和A2B2）。但实际上还可能出现其他的组合（如A1B2或A2B1）。如果我们将两个位点重组的概率用c来表示，那么c = 0.5就意味着两个位点完全不相关联，c < 0.5就意味着两个位点存在关联性。

所以连锁不平衡就是两个等位基因在群体中非随机的关联性。不过要注意，两个在物理上很近的位点不一定是连锁不平衡；而两个在物理上不连着的位点也有可能存在连锁不平衡。但是不可否认，物理上联系对两个位点的连锁不平衡起了重要的作用。

如果两个位点A和B有连锁不平衡，那么A的状态（A1）的出现可能伴随着B的状态（B1）。如果定义π为Ai的等位基因频率，qj定义为Bj等位基因的频率，在没有连锁不平衡的情况下，两个位点同时出现的概率为

gij = π * qj

但存在连锁不平衡的情况下，同时出现的概率会有所变化：

g11 = p1q1 + D

g12 = p1q2 − D

g21 = p2q1 − D

g22 = p2q2 + D

其中，D就是连锁不平衡系数。D = 0时，不存在连锁不平衡。D的取值可正可负，而且取值范围会根据π和qj的不同而不同。为了方便比较，Lewontin(1964)将D值进行了标准化：

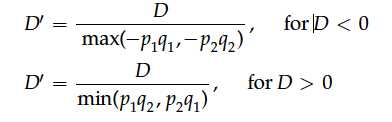
标准化之后，D’的取值就被限制在了[-1,1]之间。

另一个常用来衡量连锁不平衡的指标时r^2（Hill and Robertson 1968）：

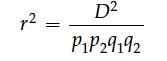
r^2的取值范围在[0,1]之间。D’和r^2虽然都是衡量连锁不平衡的，但是它们能告诉我们的信息却是不一样的。D’主要告诉我们两个位点重组情况；r^2主要告诉我们根据一个位点的状态去预测另一个位点的能力。比如：

在这种情况下（A1B1、A2B1和A2B2），D’ = 1，因为只有三种状态，除非出现了全部4种状态，否则D’总是等于1。在这种情况下，r^2 = 0.111，也就意味着在知道B位点的状态下，我们很难预测出A位点的状态。

细心的同学可能会发现，r^2乘以样本量n就会得到一个卡方统计量，可以直接进行卡方检验了。

基因组水平的连锁不平衡

前面讨论的是两个位点之间的连锁不平衡，那么如何评价一段基因序列或者整个基因组的连锁不平衡呢？

有两种方法，一种是通过数字，另一种是通过图形表示。

对于一个有n个序列，S个分离位点的群体而言，它的平均r^2可以用如下公式计算：

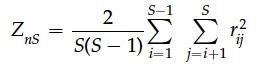
和r^2一样，Z(nS)的取值范围也是在[0,1]之间，用来表示一段序列的平均连锁不平衡（LD）情况。在没有重组的情况下，Z(nS)的值大概在0.15左右，有重组时，会造成该值降低；有选择时，会造成该值升高。所以有时候Z(nS)也被用来检测自然选择的存在。

不过我们在文献中最常见到的是用图表的形式表达一个染色体上LD的情况，如下图：

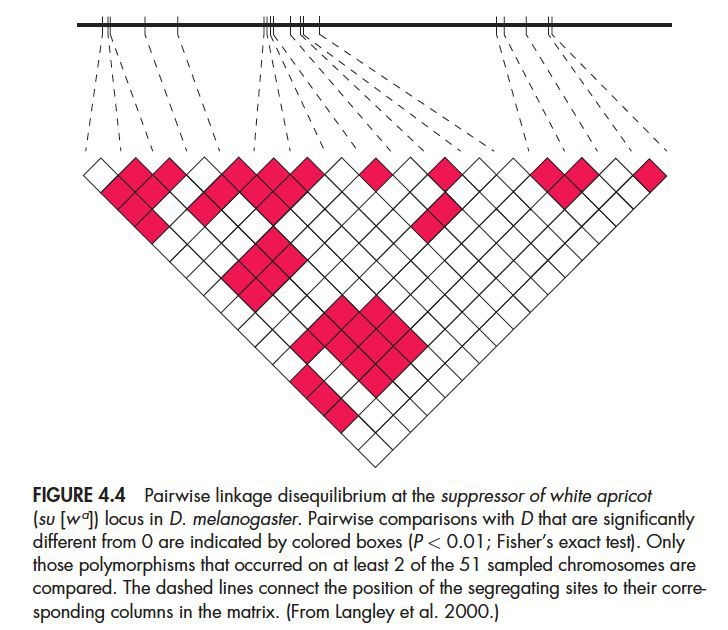
红色区域表示显著关联的位点。可以看到很多邻近的位点经常是相互关联的，但是也有很多距离很远的位点也存在关联现象。这和不同的物种有一定关系，比如在人类中，关联距离可以很远，如下图：

在一段500kb的基因片段上，有很多不同的关联区域，这些区域内的位点关联性很强，我们把这些区域称为单倍体区块 (haplotype blocks)，这区块之间是重组率很高的地方，这些地方称之为热点，不仅在人中，在其他哺乳动物中，也存在这种单倍体区块和热点。其实这和细胞的表面结构有点类似，我们知道细胞表面有很多分子并不是随机分布的，而是以“脂伐”的形式聚集存在的，完成一个共同的生理功能。染色体的很多区域也是这样，并不是随机重组，而是有重组率高的地方，有低的地方，有很多区块。

对于整个基因组还有一种描述整体LD水平的方式，就是看在多远的距离内LD能够降低到一定的阈值之内，比如在多远的距离r^2 < 0.2，或者降低到初始r^2的一半以下。如下图：

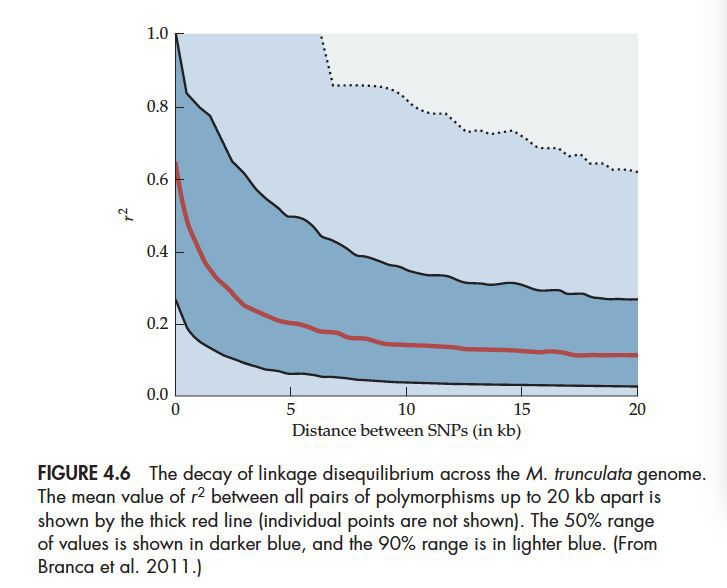
在20kb的距离内，r^2逐渐降低，大概在5kb的时候r^2均值降到了0.2以下。当然这样也只能看到基因组的整体水平，会丢失掉很多信息，比如哪些地方是重组的“热点”区域，哪些地方是“单倍体区块”等，都无法得知。

基因重组的估计

我们可以很容易的弄清分离位点的数量，那么我们能不能估计出一段序列的基因重组的数量呢？其实，这是很困难的。首先新单倍体型的出现并不一定都是因为基因重组产生的，也有可能是因为基因突变，其次很多基因重组的发生并不容易观测到，比如重组出现一个和之前已经存在的一种单倍体型。不过我们可以估计出一个满足当前单倍体情况的最小的重组次数。

估计最小重组次数的方法有两种：

（1）R(m)：根据一段序列没有重叠的最大区间数

（2）R(h)：在一个K种单倍体型，S个分裂位点的区域，重组次数R >= K-S-1，所以，对该区域的最小重组次数是K-S-1。

一般来说，R(h)要比R(m)准确一些，通常情况下R >= R(h) >= R(m)。如下图：

有4个位点，a-h共8个不同的单倍体型（K=8）。那么能够出现所有4种组合（0/0，0/1，1/0，1/1）的位点为：(1,2),(1,3),(1,4),(2,4)和(3,4)。然后去掉完全包含其他位点区间的组合：即去掉(1,3),(1,4)和(2,4)。所以剩下(1,2)和(3,4)两种组合，也就是在这个例子中最小重组数是R(m) = 2，一次重组发生在1-2位点之间，另一次重组发生在3-4位点之间。根据R(h)的计算公式，可以得到R(h) = 8-4-1 = 3，所以R(h) > R(m)。

群体重组参数

很多群体遗传事件会影响到LD，比如重组、自然选择、遗传漂变、种群结构以及突变（如果没有突变，很多重组事件可能无法检测到）。根据中性理论，决定群体重组水平的因素有两个：每个位点的重组率(c)和有效群体数量(Ne)。即

r = 4Nec

对于一个有n个样本的群体：

重组水平和LD也是有一定关系的，一般重组水平也高，LD越低。同样地，如果一个群体的群体数量越高，LD水平也越低。比如在非洲人口中，LD水平普遍比其他地区人口的LD水平低，说明人类在走出非洲的时候经历了人口瓶颈。

群体重组参数的估计

之前我们讨论过群体变异性参数 q = 4Nem，从形式上看，它和群体重组参数 r = 4Nec 很相似。不过还是有多不同之处，q在很多描述变异的公式中都会用到而且解释很容易，但是很多描述重组的统计量如K, R(m), R(h)都和r没有直接关系；其次对r的估计要比对q的估计的准确性差很多，尤其是当r的水平很低或者分离位点很少的时候，这也就意味着突变率低或者经历自然选择或群体结构变化的时候，r的估计会严重偏倚。

对r的估计通常有两种方法：矩阵法和似然估计。其中全似然估计对计算量的要求非常大，所以很多研究使用部分似然估计，降低了对计算量的要求。

（六）种群分化

https://zhuanlan.zhihu.com/p/360243643

如果种群之间没有杂交，那么任何一个在种群内改变基因频率的力量（突变、选择、漂变、迁徙）都会导致种群之间发生分化（differentiated）。分化进而导致种群结构（population structure）的出现，也就是种群内的个体之间的关系比种群之间个体的关系更加密切。

一、Wahlund effect

如何知道一个大群体中有没有种群结构的存在？可以通过Hardy-Weinberg来进行检验，如果很多个亚群被抽样，即便每一个亚群都符合Hardy-Weinberg平衡，抽样合并的总体也会偏离Hardy-Weinberg很远。而且这种偏离方向是一样的，即我们观测到的杂合子的数量总是比平衡预期的要少。这种杂合子欠缺的现象就是Wahlund effect（Wahlund 1928）。

如下图的两个种群中：

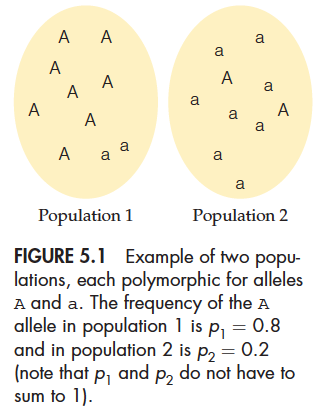
如果我们在两个群体中抽取相等数量的个体，那么在样本中A = 0.5, a = 0.5，所以理论中的杂合子频率为2Aa= 0.5，而实际上，两个群体的杂合子频率均为2*0.8*0.2 = 0.32，所以抽样的样本的实际杂合子数量也为0.32，即观测杂合子数量比预期值要少。

那么观测杂合子数量会比预期少多少呢？这和两个群体的基因频率差异有关，如果两个群体的基因频率相近，则这种差异会很小，反之，杂合子数量要远远小于预期。

当我们需要描述多个群体的时候，可以使用σ^2来表示这些群体实际与理论预期的差异大小：

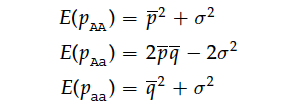
其中p(bar)和q(bar)表示所有群体的平均等位基因频率。所以σ^2是一个很好的用来描述偏离Hardy-Weinberg平衡的指标，也可以描述不同种群间的分化。

二、种群分化的衡量

1. Fst

通过上面的内容可以看到σ^2可以用来描述种群分化，但是σ^2的大小往往与平均等位基因频率p(bar)和q(bar)有关，不方便直接用来比较。这是可以将其标准化，即得到Fst:

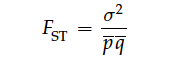
比如在之前的例子中，A和a的均值都是0.5，σ^2为（0.5-0.32）/2 = 0.09，所以两个种群间的Fst = 0.09/(0.5*0.5) = 0.36。

类似Fst，还有Fit和Fis，其中下标“i”,“s”,“t”分别指个体 (individual)、亚群 (subpopulation) 和整个群体 (total population)，具体含义可以参考方差分析的思想。

Fst能够很好的描述种群间的分化程度，Fst的取值在0-1之间。Fst = 0意味着种群之间没有分化，Fst = 1意味着两个不同的等位基因在种群中得到固定。通过下面的变化可以更好的理解Fst的意义：

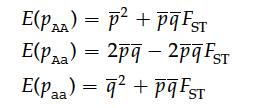
当Fst = 1的时候没有杂合子。你可以将Fst看成是衡量Wahlund effect大小的指标，或者也可以看成是由于群体不同而造成的差异（类似方差分析）。另外，对于整个基因组或者染色体而言，Fst的差异会很大，有些地方Fst小，有些地方大。Fst的分布类似于卡方检验的分布，其中自由度为K-1(K为种群数)。比如在四个种群的人类基因组Fst分布如下：

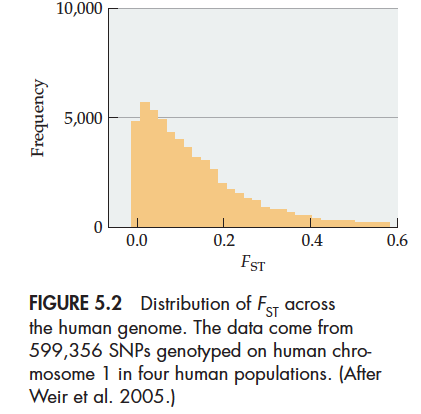
如果一个位点的等位基因数量超过2个，那么可以使用Nei(1973)的方法来计算Fst。Nei称之为Gst:

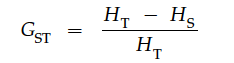
其中Ht是总样本的预期杂合子数量，Hs是各个亚群预期杂合子的平均值。

2. 其他衡量种群分化的指标

Fst的估计很容易受到亚群内部变异水平的影响，比如在染色体重组率低的区域的核苷酸多样性会降低，其Fst比重组率高的区域的要高。

Nei(1973)提出了一个统计量d(XY)来表示来自两个种群序列的差异，排除种群内部的差异。

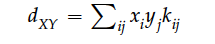
其中，x(i)表示分别来自X群体的第i个单倍体型的频率，y(j)同理，k(ij)表示相互比较的两个单倍体上碱基存在差异的数量。这一统计量是一个绝对指标，不会在受到核苷酸多样性的影响了。

除了d(XY)这个绝对指标，还有一些衍生的相对指标用来描述种群间的差异，如d(a)，有时候也称之为D(a):

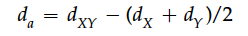
d(a)表示的是自两个种群分化以后的差异，因为它在总差异d(XY)中减去了分化之前累计的差异。d(a)受到物种内的变异影响很大，所以是一个相对指标。比如下图，（A）是由一个平均重组水平的位点得到的谱系图；（B）是由一个重组水平很低的位点得到的谱系图。

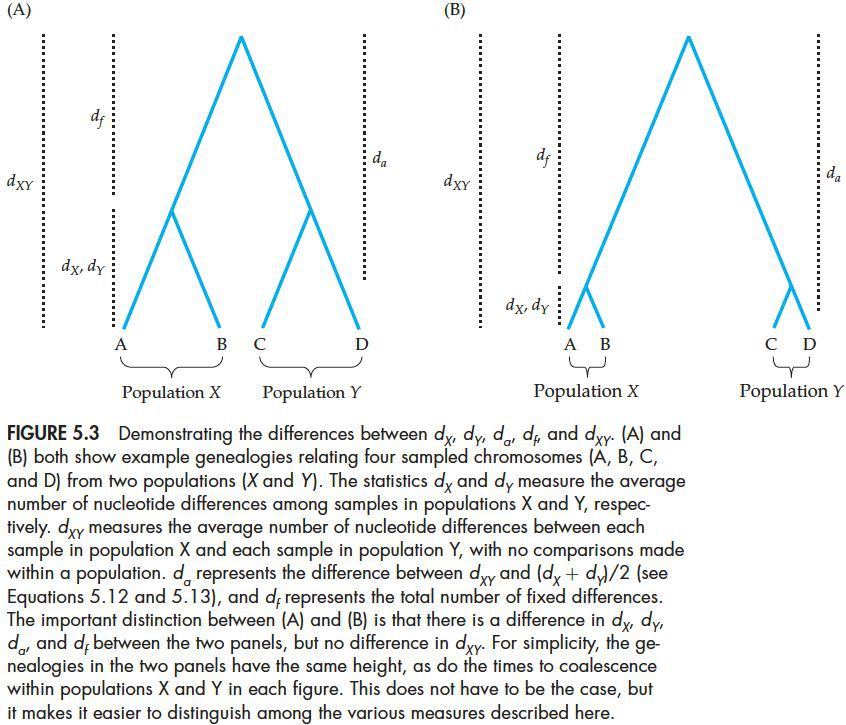
种内差异水平和最近祖先的距离成比例，离最近祖先越近，种内差异水平越小，反之越大。在A中，d(X)和d(Y)很大，这就相应的导致了d(a)和d(f)变低。对于B来讲，由于该位点的重组率低，所以种内差异距离很小，相应地d(a)和d(f)变高。所以d(a)是一个相对指标，受种内差异的影响很大，有时候并不适合用来比较种群分化程度。

三、种群分化程度的检验

如前面所述，对于知道基因型的种群，可以通过Hardy-Weinberg平衡来检验是否存在种群结构，如果不知道基因型，也可以通过等位基因频率比较。

当然，我们还可以根据Fst来检验，无效假设为Fst = 0。同时要注意样本量对统计结果的影响，如果我们有足够大的样本量，那么Fst=0.001这么小的差异也可能被检验出来，而实际上这么小的差异在我们的研究中没有太大意义，我们甚至可以将它们合并起来作为一个群体来研究。

一般来讲，Fst的分级为: 0–分化可忽略–0.15–中等分化–0.25–分化很大–1

（七）进化对种群分化的影响

https://zhuanlan.zhihu.com/p/360244093

进化通过改变种群基因频率来影响种群的分化，进化的驱动力来自：突变、自然选择、遗传漂变和迁徙。其中突变的影响很小，所以种群分化主要是受自然选择、漂变、迁徙以及它们之间的相互关系影响。

1、自然选择对种群分化的影响

对种群分化有影响的自然选择的类型包括：弱负向选择(weak negative selection)、平衡选择(balancing selection)和正向选择(positive selection)。弱负向突变能够使基因频率保持在较低的水平，平衡突变可以使变异在任何的频率水平在群体中长期维持。另外，强负向选择会将有害变异剔除种群，不会改变群体基因频率，对种群分化影响不大。受到弱负向选择和平衡选择的位点的Fst要比没有选择的情况下小，所以它们阻碍了种群的分化。下图是负向选择对种群分化的影响：

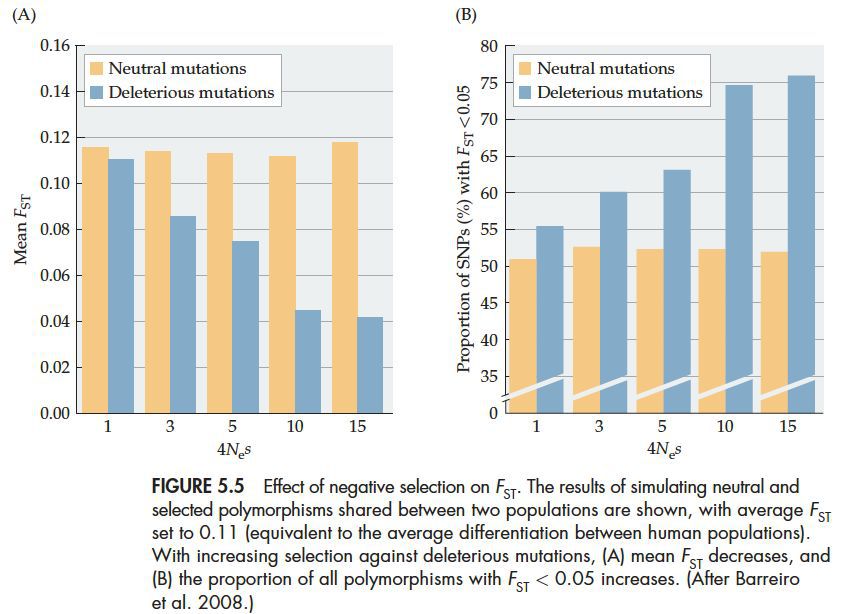
随着对有害突变的选择性增加，种群间的Fst逐渐减少，没有种群差异的SNP位点逐渐增多。

正向选择对种群分化的影响很大。如果种群内的两个亚群有完全不同的选择方向，那么受到选择的位点的Fst可能会达到1.如下图

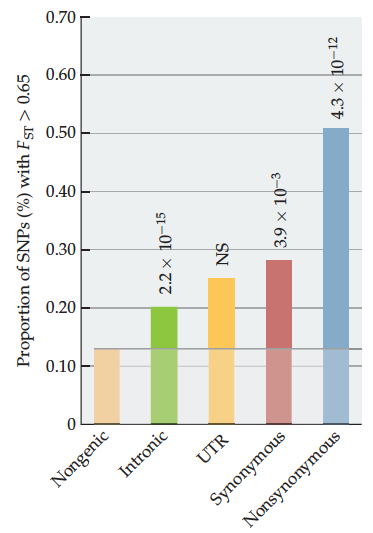
在四个人类群体的SNP分类中，非同义突变的位于Fst分布的右侧（Fst>0.65），说明非同义突变对种群分化有很大的影响。

2、漂变和迁徙对种群分化的影响

前面讨论的自然选择主要是对有选择压力的位点的影响，对于很多中性位点来讲，漂变、迁徙以及与选择位点的关联性才是主要的影响因素。

漂变和迁徙时两个效果相反的作用力。我们将通过两个模型来弄清这个为题：迁徙模型和孤岛模型。

迁徙模型：种群间的迁徙能够补偿种群间的基因频率的差异；而漂变则会增大这种差异。假设在一个种群的所有亚群中都达到了迁徙-漂变平衡(migration-driftequilibrium)，那么对于常染色体位点的Fst：

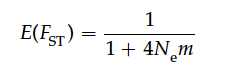
其中Ne表示每一个亚群的种群数量（假设他们都相等），m表示每一代中每个个体的迁徙概率。在假设没有迁徙的情况下，m=0，种群间的Fst=1；随着m的增，Fst趋近于0，也就是亚群之间不再有种群分化（下图A-C）。注意，这是在假设迁徙-漂变平衡的前提下，很多时候这一前提条件并不能够满足。

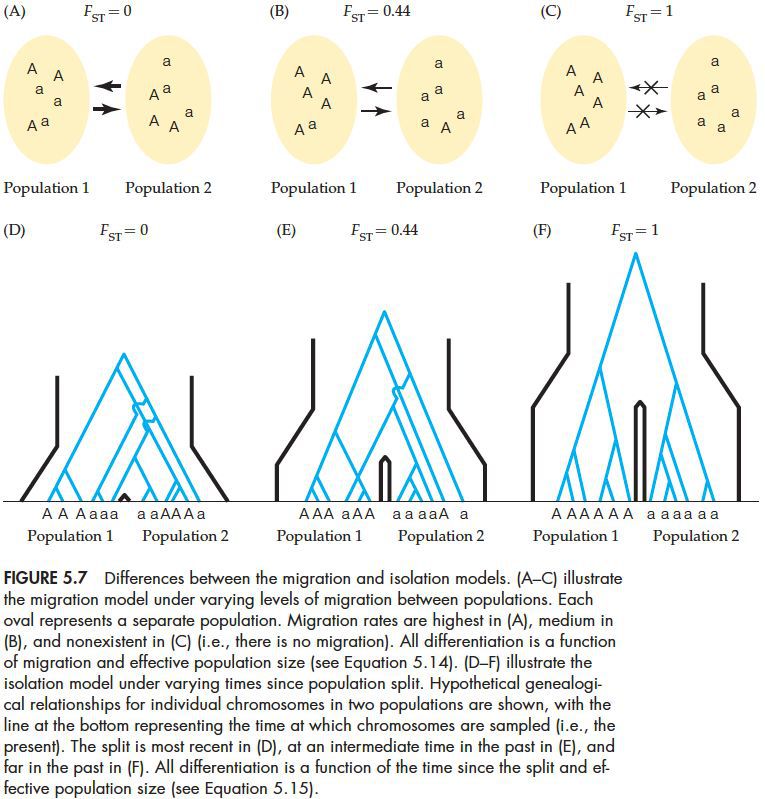
孤岛模型描述的是种群分开以后他们之间不再有迁徙的发生。在种群分离的时候，各个亚群有相似的基因频率，但是分开之后经历不同的选择或者遗传漂变，导致了各个亚群之间基因频率不同。这个过程也叫做“谱系重塑”(lineage sorting)，当然，这是一个很漫长的过程。有研究估计大概经过9-12Ne代之后，常染色体多态性才会出现95%的差异。

在孤岛模型中，有两个很重要的参数，一个是分离时间，t；另一个是有效种群数量，Ne。种群之间的分化程度Fst可以表示为：

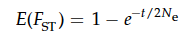
其中t为世代数。分离时间越久，种群间的差异越大，有效种群数量越大，种群差异越小。任何导致有效种群数量变化的因素都可以影响种群分化的过程，比如人口瓶颈，会导致人口减少，促进种群间的分化。同样的，性染色体的有效群体数量要比常染色体少，因而性染色体上的位点在不同群体中分化程度要更大。

既然漂变和迁徙都会影响种群分化的过程，那么对于两个群体怎样判断到底是漂变还是迁徙造成的呢？

有研究认为迁徙比漂变对种群分化的影响更大。目前也有很多模型用来探讨这个问题，比如IM，IMa和IMa2等方法来估计在种群分化中迁徙的影响。但是这些方法都有很多局限性，因为它们都有很多难以满足的条件假设，比如没有选择的存在，不存在基因重组等等，另外很多进化过程产生的效果很相似，通过有限的数据很难将它们区分开来。

还有一些方法通过模拟的方法提出假设，根据Fst或者d(XY)来判断两个群体之间是否存在迁徙。还有一个根据连锁不平衡（LD）来判断，认为如果两个群体不存在迁徙，那么该群体中的基因经历很多次的重组，LD不会很高，反之迁徙会造成该群体内LD升高。

3、群体的识别

一个样本中的个体是否来源于同一个群体，如果不是，那么是来源于哪些群体？弄清这些问题有很多实际用途，比如相关性研究中通过对不同来源的个体进行分层来控制混杂因素，比如研究濒危物种的状态，比如了解杂交区域的信息等。很多方法可以用来识别群体来源，主要思想就是最小化Hardy-Weinberg不平衡以及最小化连锁不平衡。STRUCTURE软件是最常用的分析软件。这其中最关键的一个因素是找到最优群体数量（K），同时避免模型过度拟合（Overfitting）。

（八）溯祖谱系

https://zhuanlan.zhihu.com/p/360244638

1、DNA序列模拟

理想情况下，我们可以通过计算机模拟出各种模型的种群，不同的选择压力，不同的群体结构等各种感兴趣的参数，模拟的结果和在自然群体的等价。这一个过程重复成千上万次，以此来找和实际观测数据最相符的模拟条件（极大似然估计）或者以此建立无效假设进行统计检验。

向前模拟（forward simulation）：模拟开始于二倍体群体，选择一个合适的模型，设定突变参数、重组参数、交配、自然选择参数等，持续很多代之后，群体达到了平衡，然后我们从这个群体中抽样。这种从开始随时间演化的模型就是向前模拟。

这种模拟方法的效率很低，我们需要的是抽样样本，但实际上我们把整个群体都模拟了。于是出现了另一种模拟方式，向后模拟（backward simulation，coalescent simulation），它是根据谱系关系来模拟的，从当下开始，向过去模拟，所以叫做向后模拟。它仅仅考虑一个样本，不需要考虑整个群体，所以模拟效率很高。很多小软件都可以进行向后模拟：

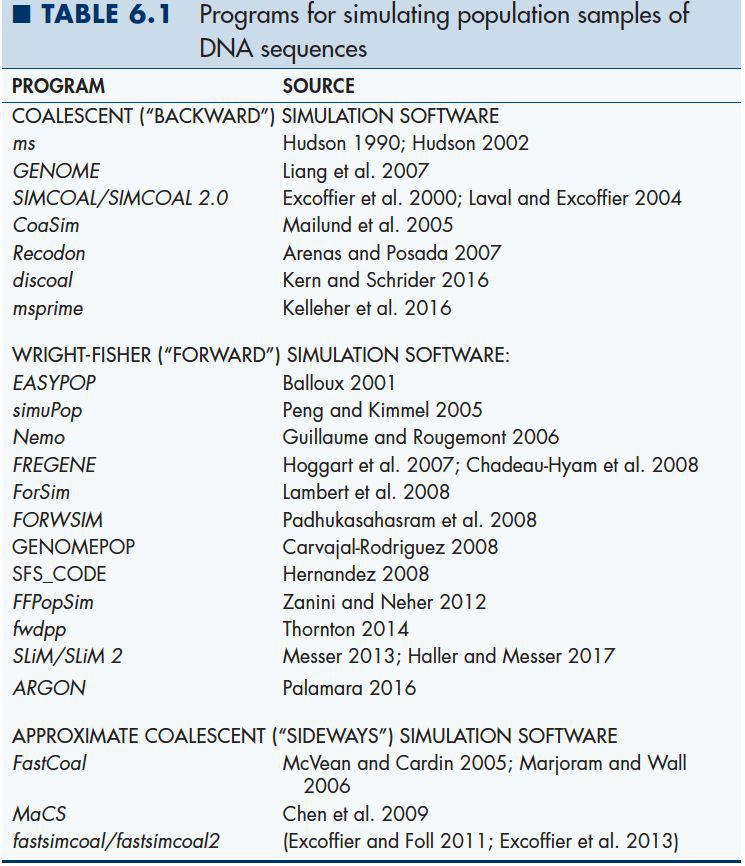
其中，ms, SLiM/SLiM2, FastCoal等是比较常见的。

当然，不管是从生物学角度还是从计算的角度，向后模拟也有一些局限性。首先，它的前提条件是样本量n要远远小于有效群体数量Ne，如果不满足这个条件会造成模拟结果的偏倚。其次，它仅仅是模拟了一个没有选择的群体中的小样本，因此除了样本信息外，我们不能够得到其他有关该群体的信息。从计算的角度来说，如果模拟的基因区域很大，或者该区域有很高的重组率，那么向后模拟依旧效率很低。

所以或许在未来，随着计算机运行速度的提升和DNA测序技术的进步，向前模拟才是最好最广泛使用的模拟方法。

2、模拟溯祖

溯祖谱系

一个群体的任何一对同源染色体都有一个共同的祖先。两个序列随时间倒推到过去的某一个时间点，在该时间点它们是同一个来源，就可以说该对序列溯祖到同一个谱系。下图是模拟的10个单倍体的演化关系：

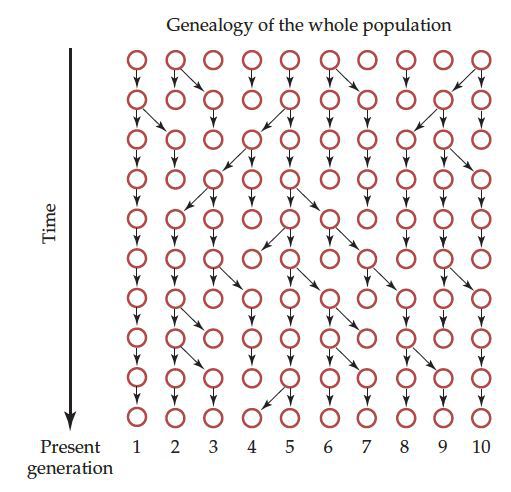
其中5个单倍体为的最近共同祖先为：

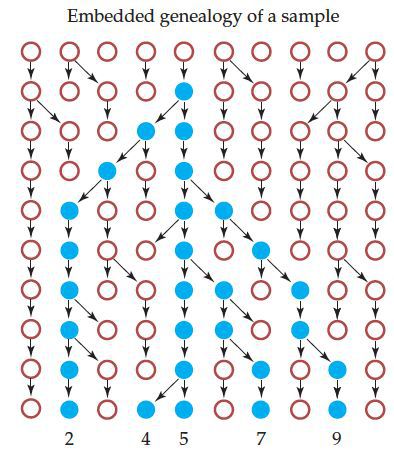
那么这5个单倍体的谱系关系可以表示为：

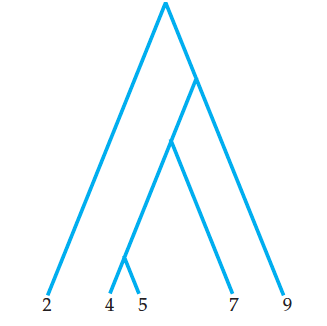
参考：线粒体的夏娃

通过溯祖可以知道一个样本的谱系。在一个谱系图中，分支越多的地方，间隔时间越短。如下图：

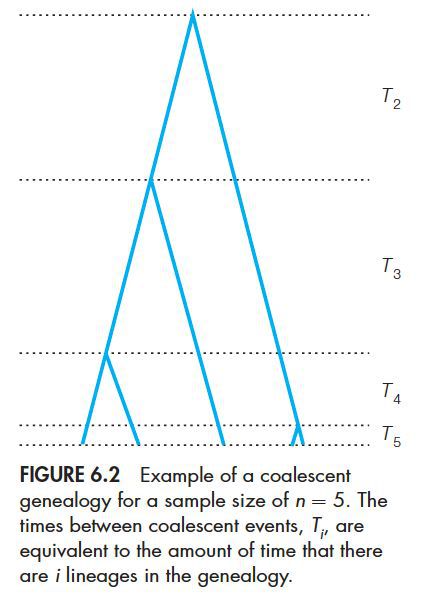
不管有没有突变的存在，溯祖谱系图都可以建立起来。当然，我们可以把突变加入建图，通常有两种方法：第一种是fixed-S方法，即事先设定突变数量S，然后我们根据各个分支的长度的不同，在谱系图底部加入数量不等的突变；第二种方法是根据突变参数q=4Nu生成不同数量的突变。下图是含有突变位点的谱系图，包括4个染色体的6个突变位点。

可以看出，突变发生的越早，越靠近根部，样本中含有该突变的个体越多。

需要注意的一点是，尽管谱系图和系统发生图有很多相似的地方，但是它们有很大的不同。我们通过“建树-添加突变”能够建立一系列的可能的谱系，它们并不一定是真实关系的反应。

谱系量化的几个参数：

（1）聚合概率：分支越多，聚合的概率越大

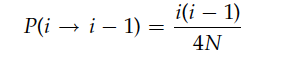
（2）聚合时间间隔：分支越多，聚合时间间隔越小。所以越靠近底部，聚合时间越小，靠近顶部，聚合时间越长。

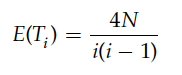
（3）谱系高度：样本量越大，谱系高度越高，并逐渐接近4N。

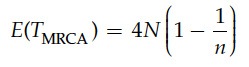
（4）谱系总长度：即谱系树所有分支的长度和，它决定了群体中能够观测到的突变的数量。样本量越大，总长度越长。

根据谱系关系，可以推算出，一个群体中有一个突变位点的比例是最多的，其次是有两个突变位点，再次有三个，依次类推，直到n-1。对于祖系状态已知的位点，在没有选择的情况下，等位基因频谱为：

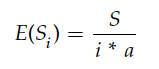
其中S表示分离位点的数量，a为：

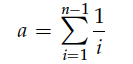
比如当n=11个样本中有S=28个分离位点，其等位基因频谱为：

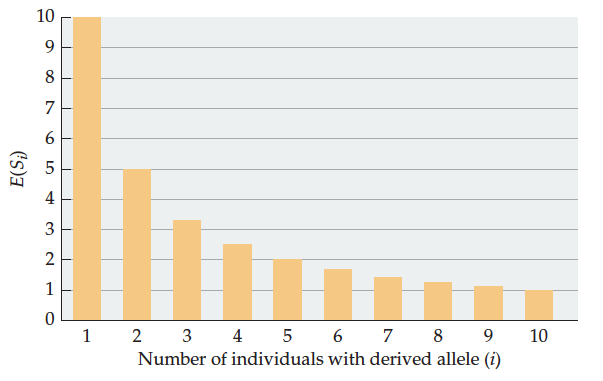
如果祖系状态未知，可以使用下面的公式计算：

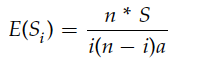
等位基因频谱在分子遗传中有很重要的应用，知道了在没有选择情况下频谱的形状，可以使我们判断一个群体是否经历自然选择，是否存在群体结构。

但是当我们的样本量比较小的时候，就会存在抽样偏倚问题。中等频率的基因更容易出现在我们的样本中，而低频率的基因很难在样本中发现。所以即便没有自然选择、没有群体结构，我们的样本中也可能出现也预期不一致的等位基因频谱。如下图解释：

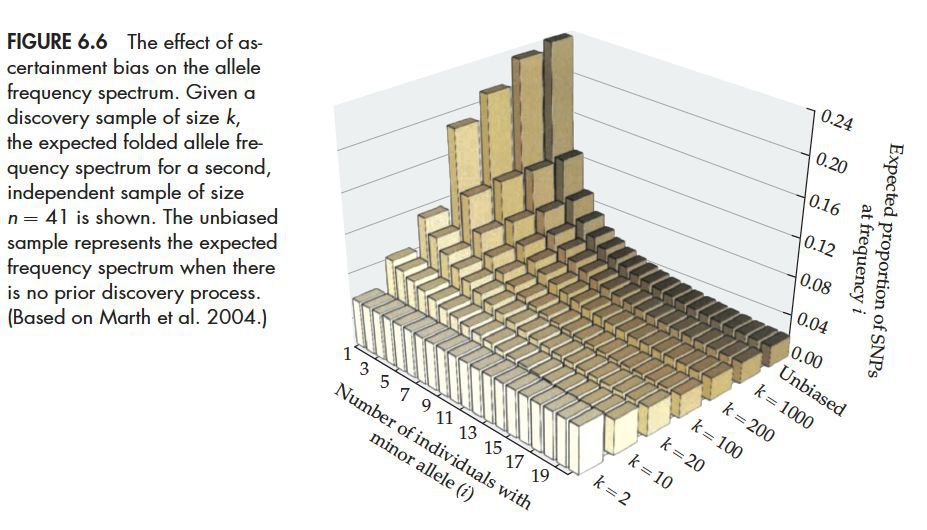
我们根据一个样本量k=1000的样本判断的SNP来作n=41的样本的频谱图，要比k=10时更接近于理论情况。

（九）定向选择

https://zhuanlan.zhihu.com/p/360246474

碱基替换率

碱基替换率就是新的碱基以什么样的速度在种群中固化下来，通常用k表示，单位一般是每代或者每百万年，它决定了两个序列的分化所需要的时间。两个序列间的遗传距离可以用一下公式表示：

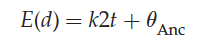
其中t是物种自分化之后时间（序列的分化早于物种分化，如下图），通常为了简便，我们描述一个位点，这样就不用在考虑序列长度的问题了。在一个基因位点内，k表示平均的碱基替换率。theta(Anc)表示在物种分化之前累计的序列变异程度。有时候该项相对比较小的时候，可以忽略，将上述公式写为：

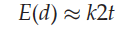
也就是说时间越久，替换率越高，序列之间的分化就越快。

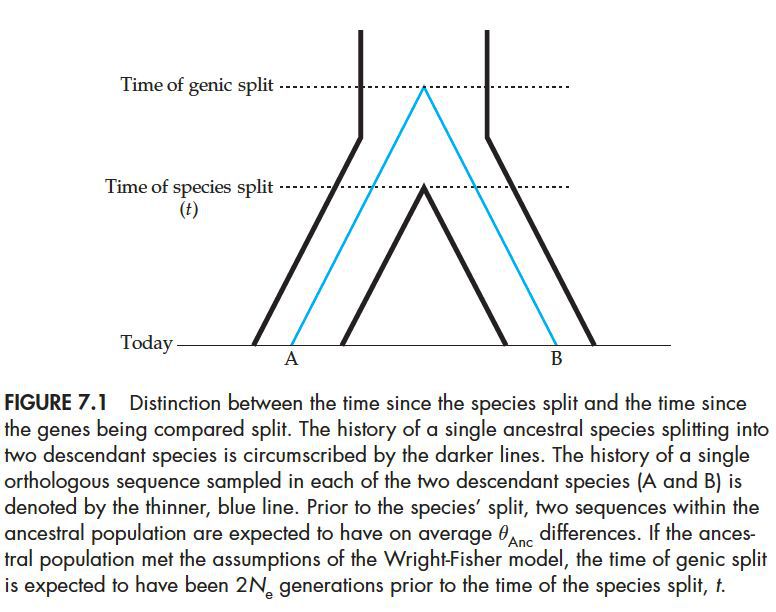
第一个影响碱基替换速率的因素是突变的固化概率。对于一个中性突变来说，它在种群中得到固化的概率和它开始出现时的频率时一样的。在2N的群体中出现一个突变，它的固化概率是1/2N。

对于一个有利突变来说，如果种群足够大，它的固化概率是：

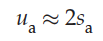
其中s(a)是突变在杂合子中的选择优势，2s(a)是突变纯合子的选择优势。

对于一个有害突变（有害程度不大），其在种群中固化的概率是：

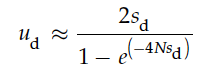
其中s(d)是突变在杂合子中的选择劣势，2s(d)是突变纯合子的选择劣势。

对于稍微有害或者稍微有利的突变，其在种群中得到固化的概率和中性突变相差无几，所以这些位点也通常被统称为“近乎中性”。

第二个影响碱基替换速率的因素是突变的数量。

总结一句话就是，在只考虑中性突变的情况下，碱基替换的速率和突变速率是相当的，这和种群大小没有关系。如果考虑非中性突变，种群数量就起到了关键因素，对于有利的突变在大种群中更容易固化，反之，对于有害的突变，在小种群中更容易得到固化（考虑一下遗传漂变就很容易理解这一点了）。

序列分化d的估计

之前我们讨论过使用d表示直系同源序列的遗传距离，也就是将每个物种中的不同位点两两比较，然后除以总的核酸位点数。但是这种方法在遇到多序列比对时，容易出现问题，我们知道在多序列比对中有很多gap，而有gap的地方时不被d统计量考虑在内的。如下图多序列比对：

在多序列比对时，第一个序列和第二个序列的d = 3/11 = 0.273（剔除1，2，9，10四个位点），但是如果只有这两个序列比对，那么d = 3/13 = 0.23（剔除1，2两个位点）。所以这种情况会导致序列分化程度估计的偏倚。

在计算d的时候还有两个重要的问题需要考虑。第一个是我们是从每个物种中选取的一个序列，那么这个序列并不一定代表已经固定了的位点的碱基，还有可能是一个多态性位点的碱基。如下图：

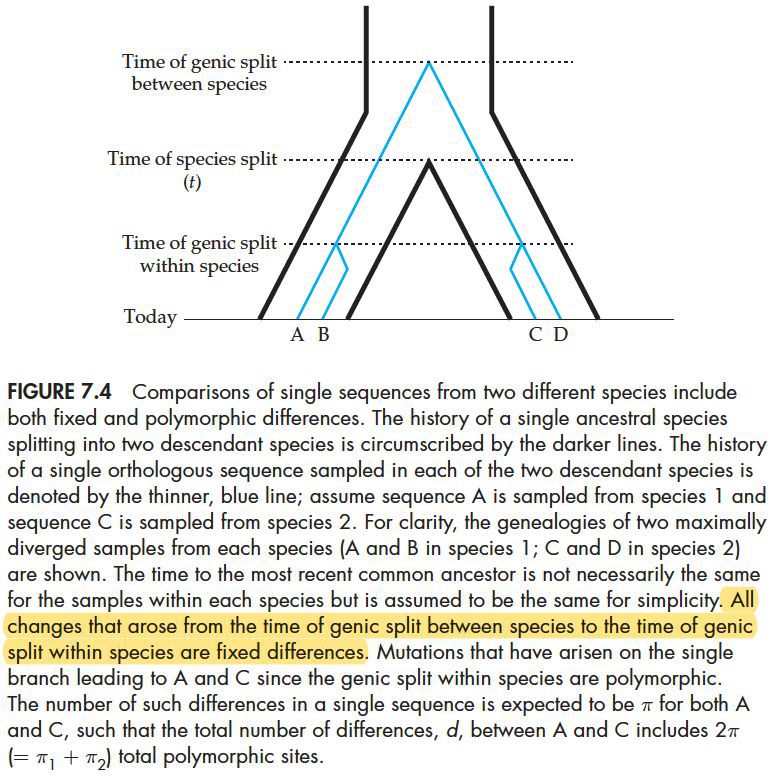
也就是在比较序列A和C的分化程度时，A和C中仍然有2p（假设A和C的多态性位点都是p）个多态性位点，这些多态性位点是在物种分离之后形成的。在序列分化之后和物种分离之前形成的是已经固化的位点差异。所以要计算两个物种固化位点的分化d* = d - 2p。

第二个在计算d的时候要注意的是，对于两个关系很远的物种，一个位点有可能经过了多次突变，甚至变回和之前一样的，这就会低估两个序列的差异性。这个时候考虑使用Jukes-Cantor方法进行校正。

使用dN/dS识别自然选择

dN（又称Ka或KN）表示非同义突变SNP数/非同义位点数，即非同义突变率；dS（又称Ks）表示同义突变SNP数/同义位点数，即同义突变率。比如：

当第三个位点发生突变时，有2/3的可能是非同义突变，有1/3的可能是同义突变。那么这个密码子也称之为“二重简并性“密码子。另外对于这个密码子的前两个碱基都是非同义突变，没有简并性，即3/3非同义突变和0/3同义突变。非同义突变的数量Nc= 2/3 + 3/3 + 3/3 = 8/3；同义突变的数量Sc= 1/3+ 0/3 + 0/3 = 1/3。

当然，上面没有考虑碱基替代倾向的问题。比如上述例子中，AàG的碱基转换transition可能比AàC和AàT的碱基颠换tranversion更容易发生，这是该碱基位点的同义突变可能高于1/3，这是就需要对结果进行校正了。

如果一个密码子中的突变不只是一个，那么这种情况就比较复杂了。到底哪一个先进行的突变，就不得而知了，比如：TTTàGTA，可能有两种突变方式：

其中第一种方式有1个同义突变和一个非同义突变（Nd=1, Sd=1），而第二种方式两种都是非同义突变（Nd=2, Sd=0），这个时候也需要对结果进行校正。

现在越来越多的方法是使用似然估计来计算dN，dS。

当然，我们这儿更关注的是自然选择是怎样影响dN，dS的。对于一段序列，有如下公式描述自然选择对dN的影响：

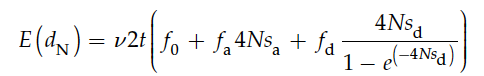
其中f0,fa和fd表示中性突变、有利突变和有害突变所占的比例，sa和sd表示有利突变和有害突变的选择压力。也就是说dN的大小和突变率v，以及分化时间t成比例，突变率越高，分化时间越久，dN越大。同时对于有利突变，有利突变的比例和选择压力同样会增大dN的值；对于有害突变，只要选择压力不是太大，也能增大dN的值。

对于dS的值可以用以下公式表示：

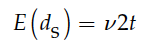
也就是两个序列同义位点突变数只与突变率和分化时间成正比。

如果我们要考虑自然选择的影响，似乎只要考虑dN就可以了，dN越大，说明该序列收到的自然选择越大。但是我们忽略了一点，那就是在一段染色体序列中，各个地方的突变率是不同的。所以即便有自然选择，但是如果突变率很低的话，也可能不会出现很大的dN值。Kimura（1977）提出了用dN/dS的比值来识别自然选择，根据上面的两个公式可以看到，dN/dS比值消除了突变率不同带来的影响。

下图是两种拟南芥11492个直系同源基因的dN/dS­分布。

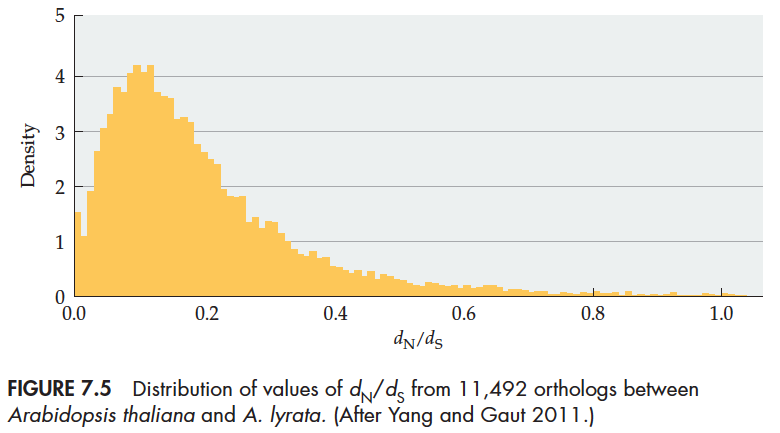
可以看到，dN/dS的平均值大概在0.15-0.25之间，也就是说至少有75%-85%的非同义突变是有害的。另外dN/dS的值大小还与种群数量有关系，例如大鼠和小鼠之间的dN/dS为0.14，而人和黑猩猩之间的dN/dS为0.20，在没有充分证据证明灵长类动物有更多有利突变的前提下，我们认为这种差异是由于种群数量不同造成的，灵长类比鼠类的种群数量小，因为dN/dS比较大。

根据dN/dS来判断自然选择的类型存在一些缺陷，比如一个蛋白质的不同部分可能受到不同类型的选择，一部分受到很强的正向选择，还有一部分受到很强的负向选择，编码该蛋白的基因区域总体上可能是dN/dS<1，但是某些区域可能dN/dS>1。一般认为：

还要重申一下，dN/dS= 1并不代表着一定是中性，很多自然选择的联合作用可能表现出dN/dS= 1的结果；另外，对于一些没有固化的中性突变，也会出现dN/dS< 1的情况。dN/dS通常受样本量大小、群体历史过程等的因素影响比较小。

通过基因组多态性来识别自然选择: McDonald-Kreitman(MK)检验

MK检验有四个基础变量（类似卡方检验）：

MK检验的理论基础是根据分子进化中性理论，来比较多态性位点和固化位点的同义和非同义突变的差异。在中性理论下，四个变量的期待值为：

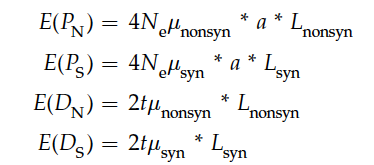
如果所有的多态性位点和固化位点都是中性的，那么各自同义突变和非同义突变的比值应该是相等的，这是MK检验不会有统计学差异。比如下面的例子：

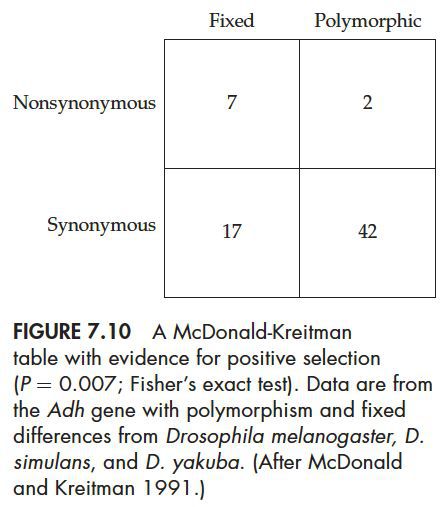
多态性位点中非同义突变和同义突变的比例为2:42，在固化位点中这一比例为7:17，也就意味着固化位点有更多的非同义突变，MK检验p=0.007，所以提示可能有适应性的自然选择存在。当然如果多态性位点有过多的非同义突变，也可能导致这种情况出现，这是时候可能是因为有很多弱有害突变造成的，它是非同义突变，但是又不至于很快被淘汰掉。

不过如果存在很多这种弱有害突变，在多态性位点出现很多非同义突变，就会降低检测正向选择的能力。这个时候我们可以剔除那些频率较低的多态性位点（比如<15%）,这个时候就能够大大提升检测能力。

同样地，采样因素和群体历史因素对MK检验影响不大，但是MK检验假设中性突变率对同义突变和非同义突变都不随时间发生改变，这一假设在很多时候并不能满足。

中性指数（neutrality index, NI）是对MK四格表形式的变形：

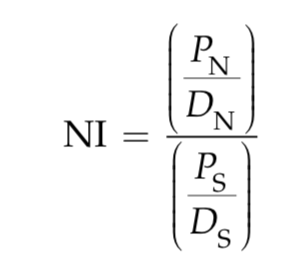
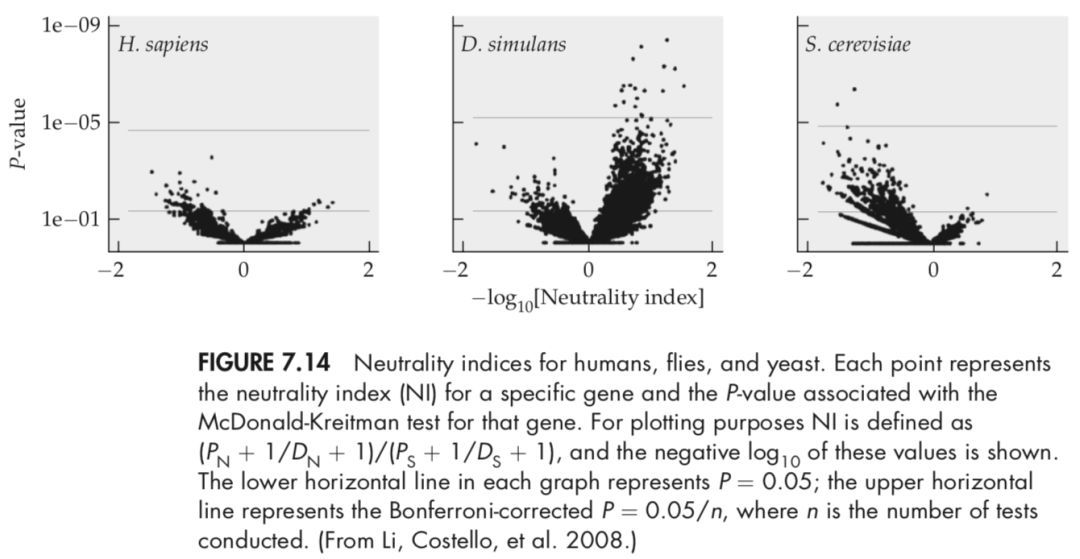
NI > 1表示过多的非同义突变多态位点，NI < 1表示过多的非同义突变的固化位点。在中性条件下，NI =1。不过为了直观方便的表示，通常将NI作负对数变换，这个时候正值表示正向选择，负值表示负向选择。如下图，是三个物种（人、果蝇、酵母菌）的NI负对数值，可以看出在果蝇中，有很多正向选择的基因存在。

（十）关联选择

https://zhuanlan.zhihu.com/p/360246853

如果一个位点受到自然选择，该位点的等位基因频率会改变，那么和该位点相关联的位点的等位基因多态性也会受到影响，这就是关联选择 (linked selection)。

正向选择所导致的关联选择

正向选择会提升有利等位基因的频率，会导致该等位基因附近核算多态性降低，这种情况也被称为selective sweep或者搭便车hitchhiking。Selective sweep就是指含有有利突变的单倍体受到自然选择，频率在群体中迅速增加，同时导致该染色体区域基因多态性降低。selective sweep又分为hard sweep和soft sweep。前者是在受到自然选择的单倍体只有一种，自然选择在染色体上出现很明显的印记；后者是在受到自然选择的单倍体有多种，核酸多态性降低不明显。soft sweep常发生在现有多态性位点 (standing genetic variation)上，比如因为环境的改变，使得原来一个中性的等位基因变成有利等位基因，这时群体中会有多种受选择的单倍体，产生soft sweep。同时，soft sweep比hard sweep更难以识别。

下图表示一个selective sweep：

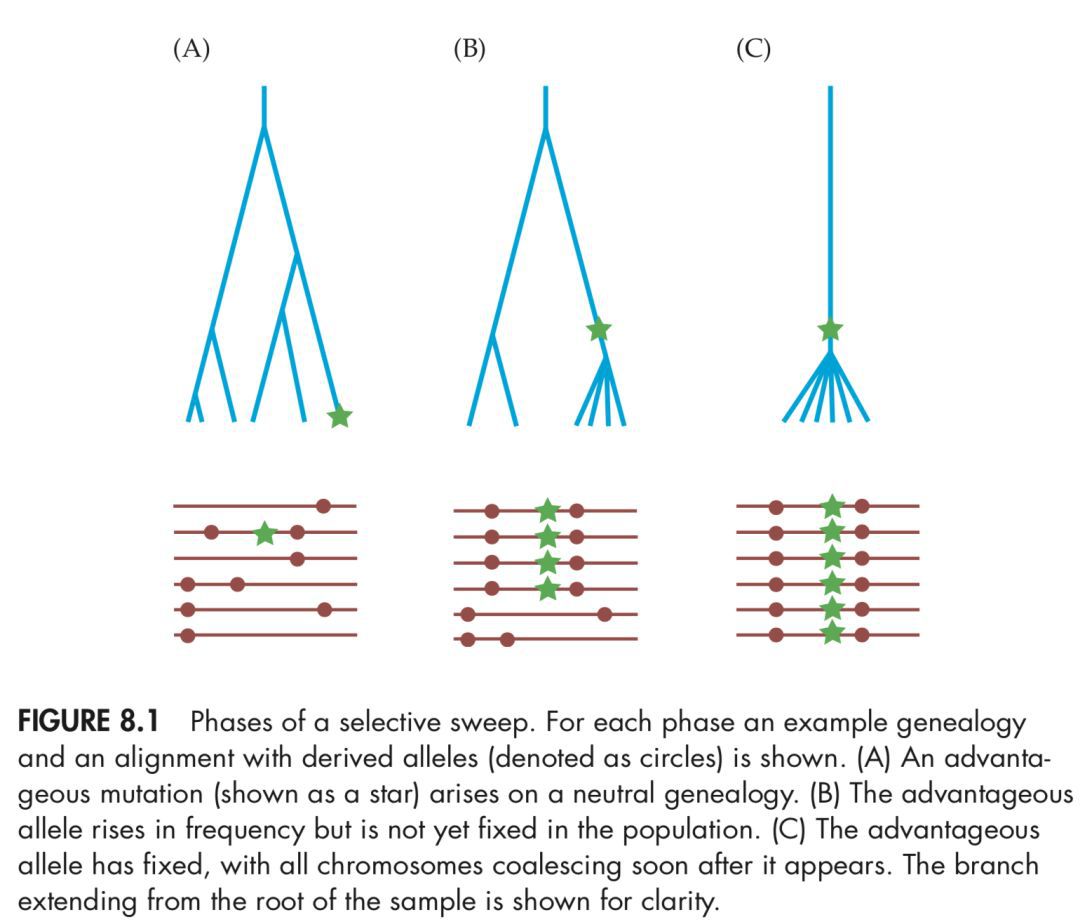
星号表示有利突变，（A）在群体中出现了一个有利突变，（B）含有该突变的单倍体频率在群体中迅速增加，（C）群体中所有的单倍体都变成了同一种。其中红色的点表示中性突变，它们因为与有利突变相关联，频率也随之迅速升高，这也就是搭便车。同时selective sweep也导致了谱系图变短。

那么哪些因素会影响核酸多态性降低的程度？（1）选择压力的大小；（2）重组水平；（3）距离selective sweep结束的时间。

selective sweep能够在基因组多态性图上表现出一个低谷。如下图：

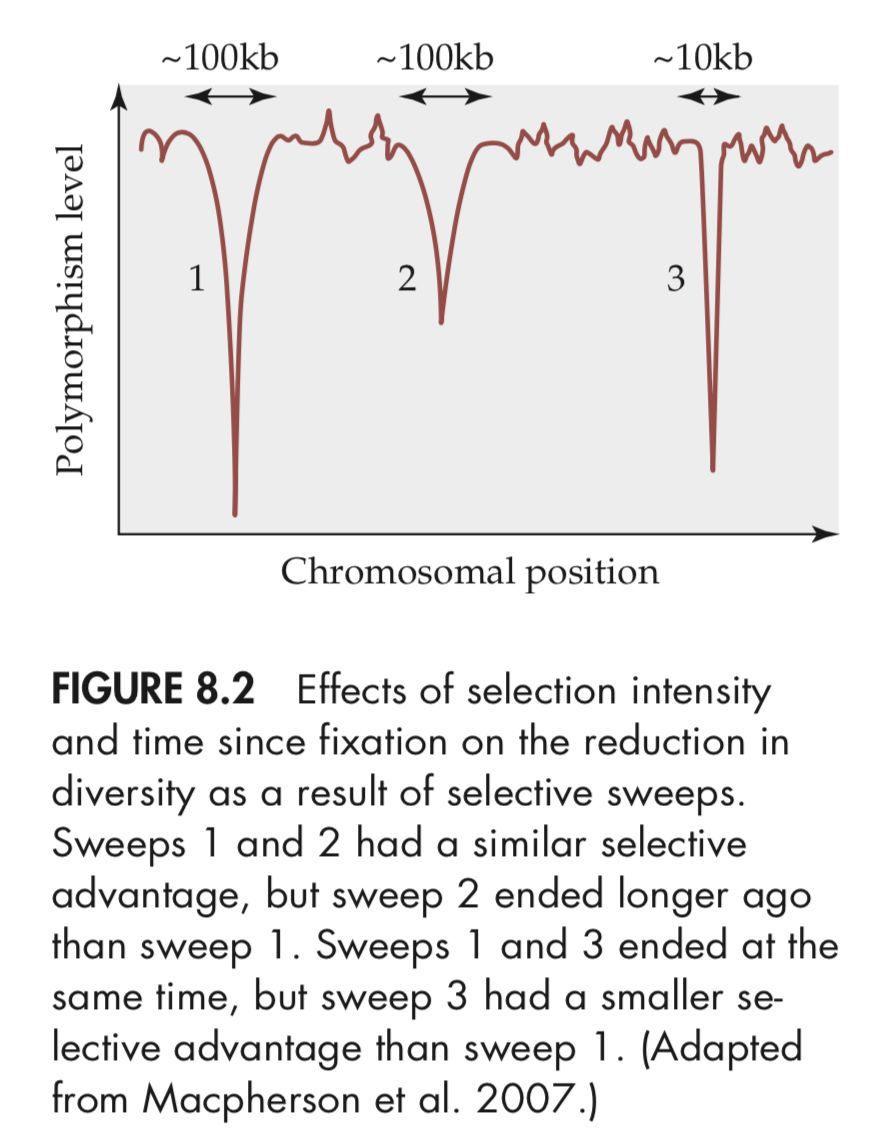
选择压力和种群大小决定了有利突变固化所需要的时间，固化时间越快，谱系图分支越短，基因多态性水平越低，所以低谷也越低。反之，如果选择压力比较弱，固化时间变长，谱系图也相对长，基因多态性水平相对较高。基因重组会使中性位点和有利突变解除关联，导致selective sweep降低基因多态性水平的作用减弱，受selective sweep影响的基因区域变小。选择压力和重组率是一对相反的作用力。一旦selective sweep结束作用，该区域的基因多态性水平会向正常水平回归。

实际中，并不是所有的selective sweep都会使有利突变固化，有些是在我们研究的时候还没有完成固化，有些是外界环境的变化是的有利突变不再有利。这些selective sweep称之为partial sweeps，比如在第一张图中的（B），就是一个尚未固化的partial sweep。

平衡选择和强有害突变所导致的关联选择

和正向选择相反，平衡选择可以造成与之相关联的基因多态性水平升高。平衡选择能够对抗遗传漂变，维持基因多态性水平。平衡选择会导致谱系图变高。如下图：

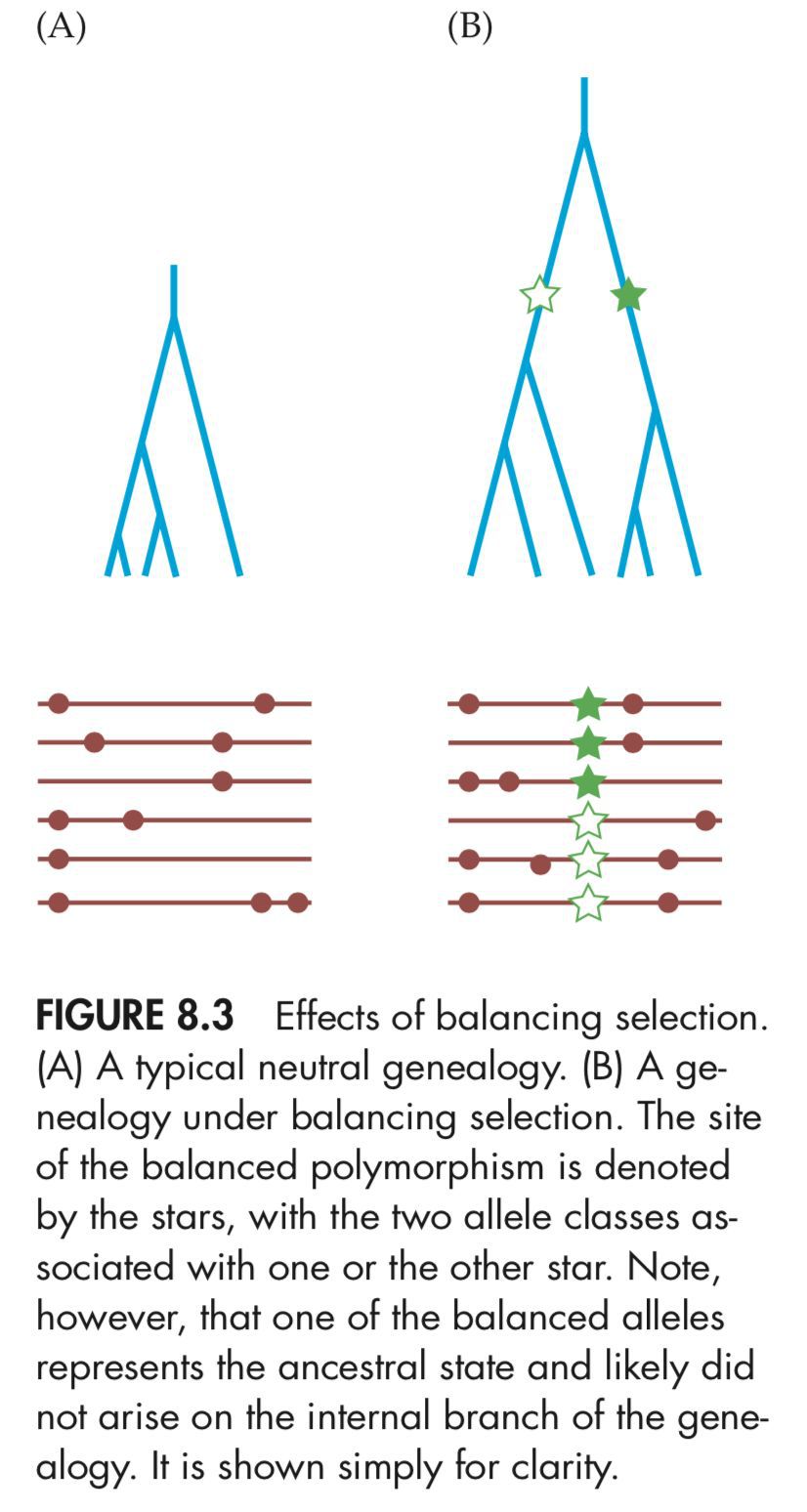
同样的，基因重组会使平衡选择的相关联区域变窄。而且基因重组对平衡关联选择很大，对于一个很老的平衡选择，基因重组会消耗掉平衡选择的作用效果，使之更难以检测。

下图是果蝇中Adh基因的平衡选择。

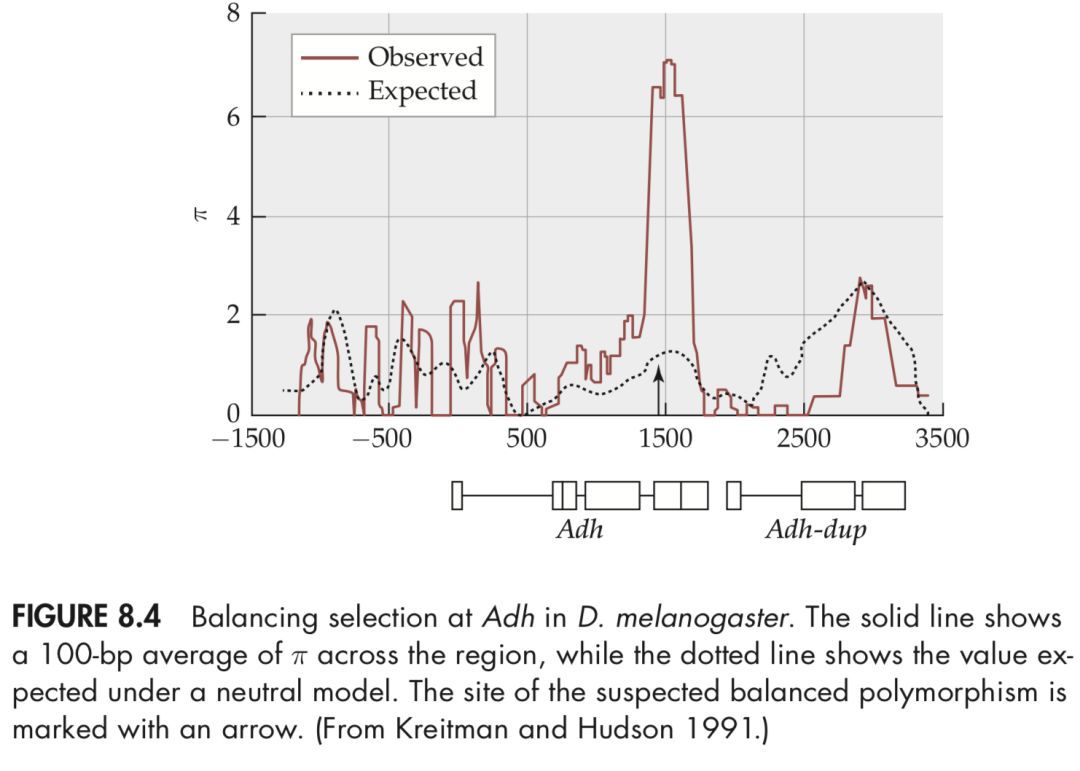
对于有害突变造成的关联选择常常被称为“背景选择”background selection，它同样能够降低相关联区域的基因多样性，降低谱系图高度。基因重组能够降低受背景选择的区域，较低的基因重组水平会增大背景选择区域，在没有基因重组的区域，如Y染色体，背景选择的作用效果非常明显。

不过需要注意一点的是，关联选择并不会影响分化水平，hitchhiking不会改变中性等位基因固化的概率。但是对于有利等位基因或者有害等位基因，它们之间的相互干扰是十分明显的，会降低有利等位基因固化的概率，同时增加有害等位基因的固化概率，这种现象也叫Hill-Robertson干扰。

（十一）HKA、等位基因频谱识别自然选择

https://zhuanlan.zhihu.com/p/360247071

HKA检验

HKA通过多态性水平检验是否存在自然选择。不过首先要强调一点的是多态性水平的变化不仅受到自然选择的影响，还会受到群体史的影响（如人口瓶颈）。所以在判定自然选择的时候一定要区别群体史。

我们知道，在中性模型中，一个群体的多态性水平为4Neu，物种间的分化距离为2tu。HKA检验最初就是回答一个问题：一个位点如果出现很低的多态性水平，那么这是因为该位点突变率低还是因为该位点最近经历了定向选择？同样的，如果多态性水平高，那么该位点可能有较高的突变率或者经历了平衡选择。近期经历自然选择的位点其物种间的分化距离是不会受到影啊的，所以我们可以以此来消除掉突变率不同对多态性水平造成的影响，从而判断是否有自然选择的存在。

HKA检验的实验设计

根据上面的原理，在HKA中我们需要两个测量指标，一个是目标物种的多态性水平（S），另一个是与该物种较近的另一个物种的分化距离（d）。HKA检验对于同义突变、非同义突变以及非编码区都是可以使用的。HKA的统计量实际上是一个卡方值，来判断多态性水平是否和分化距离成比例。如果得到一个较大的卡方值，能够拒绝无效假设，那么就可以认为自然选择的存在。

通过等位基因频谱识别自然选择

弱负向选择对等位基因频谱影响很小；强负向选择会被很快淘汰，对基因频谱影响也不大。因而这里我们只考虑正向选择和平衡选择。

正向选择

当正向选择（selective sweep）发生的时候，一个极端的情况是群体中只剩下了一种单倍体型，selective sweep完成之后的时间，种群中会出现新的突变，这些突变在群体中频率很低，因而在等位基因频谱上表现出过多的低频等位基因，频谱左偏。如下图：

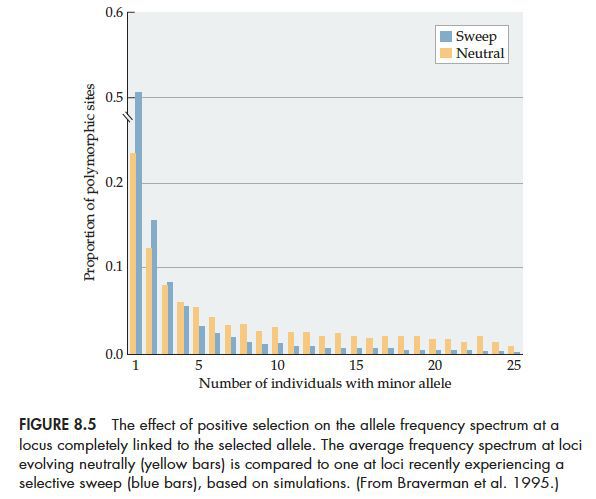
随着时间的延长，重组会使得与受选择位点相关联的中性位点得到释放，selective sweep在基因频谱上留下的印迹也会被逐渐消耗掉。

如果在selective sweep发生的过程中发生了重组，那么受选择的位点可能被关联到一个祖系状态的单倍体上，而非是一个中性突变，因而祖系状态的单倍体频率也会随着selective sweep而增加：

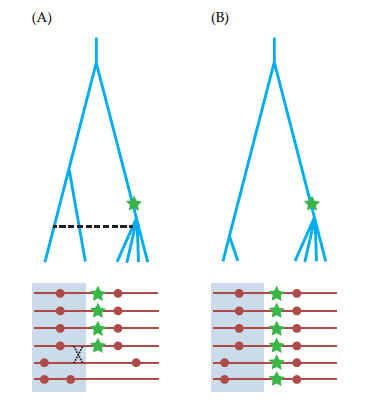
会出现另一种形式的等位基因频谱，即低频和高频增多，中间频率的位点减少：

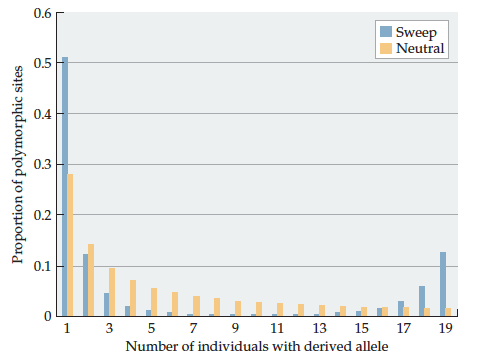
平衡选择

和正向选择相反，平衡选择会增加中等频率位点的数量，使得等位基因频谱中间凸出。对于只有两种状态的等位基因，在频率接近50%的时候是最容易识别出平衡选择的。对于时间比较短（年轻的）平衡选择，要想识别出来是很棘手的，它可能还没有达到平衡状态，因而看起来会很像selective sweep(partial selective sweep和正在进行的selective sweep)。

Tajima’s D 识别自然选择

之前章节介绍过多态性水平的描述，包括π和θw，那么Tajima’s D的计算方式实际上就是比较π和θw两种多态性表达式的差异。

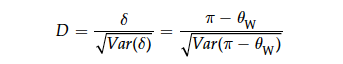
(其实很像是一个t检验)

这中性模型中，π和θw的差异接近0。Tajima’s D对数据形式要求不严格，不要求是phased数据，也不需要其他物种数据做参考。但是，Tajima’s D会受到群体历史和种群结构的影响。

一般情况下，Tajima’s D> 2或者<-2，认为是有统计学意义的，但是具体情况还要根据样本量等来判断。

当selective sweep发生时，群体中会出现很多低频突变，这个时候θw的值比π的值大，（π是通过两两比较得到的多态性统计量，而θw­是通过分离位点数量来表示多态性的），这个时候Tajima’s D就是负值（如下图）。当平衡选择发生时，种群中会有过多的中等频率的位点，这个时候θw的值比π的值小，Tajima’s D就会成为正值。

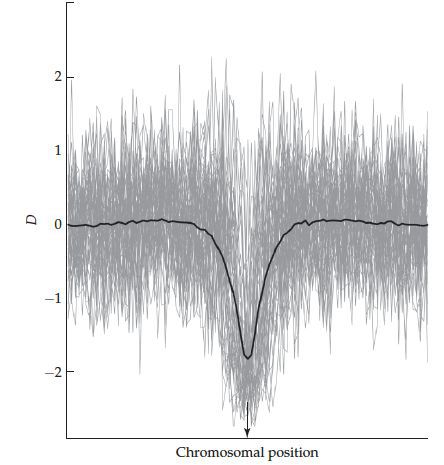
当θw和π的值相等的时候，等位基因频谱就和中性预期相一致。下图是selective sweep出现的时候θw、π以及Tajima’s D变化情况。

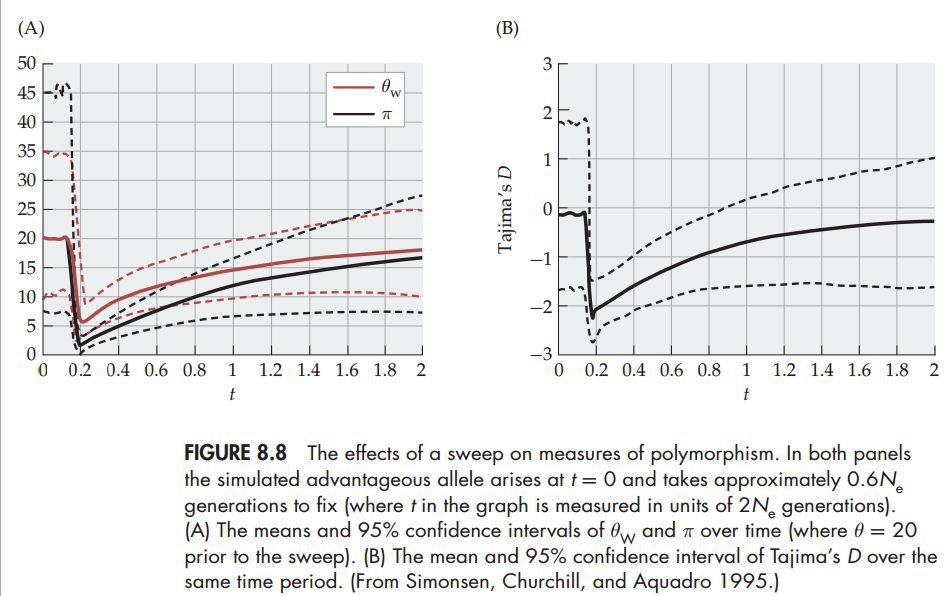
最没有出现sweep的时候，θw和π大概相等，Tajima’s D近似于0，当sweep出现的时候，虽然θw和π都降低，但是π更低，此时Tajima’s D < 0；随后θw和π增大，两者间的差异减小，最终Tajima’s D又接近于0。

Fay and Wu’s H 识别自然选择

Fay and Wu’s H同样可以用来识别自然选择，由Fay和Wu在2000年提出，表达式为：

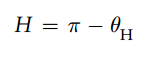
和Tajima’s D有一点区别的是H统计量没有分母，而且H特别擅长于识别高频多态性位点（即位于基因频谱右端的位点）。当sweep出现的时候，H也会变成负值。如下图：

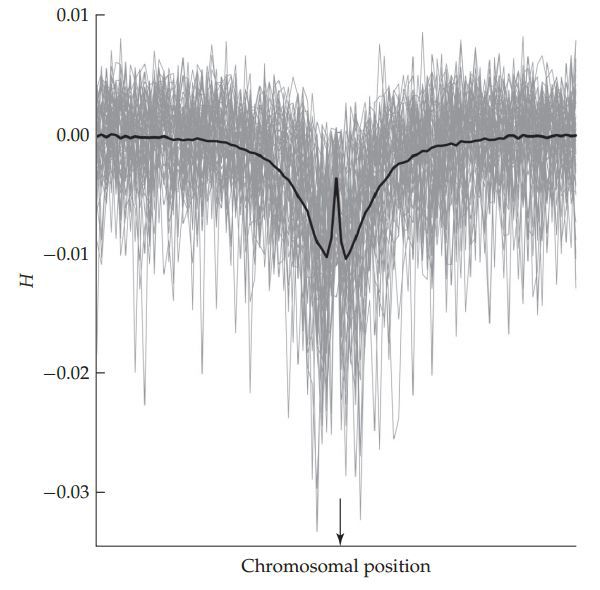
注意和Tajima’s D图不同的是，H的最小值并不是出现在受选择的位点处，而是在该位点的两侧。所以当使用H来判断受选择位点的时候一定要格外小心，要综合考虑重组率大小和计算窗口的大小。如果重组率很低，计算窗口很小，那么我们有可能会在受选择位点两侧识别出很低的H值，而含有受选择位点的窗口的H值接近于0；如果重组率很高或者计算窗口很大，那么受选择的位点可能隐含于一个H值为负的窗口里面。所以对H的解释要结合具体情况。

那么选择强度是多大时，或者需要多长时间，才能识别出自然选择？对于平衡选择，如果是很老的一个，那么重组可能会把选择遗留下的印记给消磨掉，很难再通过等位基因频谱来识别平衡突变。同样的对于定向选择（selective sweep），太早太晚都无法准确识别出选择，所以对定向选择的识别也是有一定的时间窗口的。

（十二）利用连锁不平衡识别自然选择

https://zhuanlan.zhihu.com/p/360247779

之前我们讨论识别自然选择的方法中，一般只需要知道位点的等位基因频率或者一个临近物种的基因多态性情况就够了。而且当下全基因组测序也能够提供准确的基因频率，尤其是Pool-seq的测序方法。在这一部分我们将根据连锁不平衡的情况来识别自然选择。

1. 平衡选择对连锁不平衡的影响

在一个没有选择的中性群体中，单倍体的种类（不同类型的单倍体）应该和该群体的分离位点数量成正相关关系，即分离位点数越多，单倍体的种类也越多。同时，重组会增加单倍体的种类，降低二倍体群体中纯合子数量。如果发生了平衡选择，则会打破这一现象。平衡选择会减少群体中单倍体的种类；同时在单倍体频谱（和等位基因频谱类似的概念）中，会出现缺乏低频单倍体的现象；在该区域的连锁不平衡水平也会相应增加。

2. 已经进行完成的sweep（正向选择）对连锁不平衡的影响

对于一个最近刚刚进行完的sweep，如果受选择位点附近没有重组，那么该区域大多数的变异会被从群体中剔除，同时sweep完成之后新出现的突变会增加该区域低频位点的等位基因数量，这时群体中单倍体的种类也会随着新突变的出现而增加（每出现一个新突变，都很有可能形成一种新的单倍体型）。

对于离受选择位点比较远的区域，由于重组的存在，这些区域的单倍体无法在群体中得到固化，只能达到一个较高的频率，这时就表现出该区域连锁不平衡水平的增加，群体中会出现一种主要的单倍体型，同时该区域单倍体的种类会因此减少，群体中二倍体纯合子数量增加。

3. Partial sweep对连锁不平衡的影响

即在群体中正在进行或者尚未得到固化的sweep。这和一个已经进行完成的sweep的周边的情况很像，一种单倍体型会出现升高，群体中单倍体的种类会降低，二倍体纯合子数增加。

4. 单倍体型和自然选择

为了寻找sweep，我们可以首先寻找和突变位点相关联而重组又非常少的区域。最常用的方法就是通过单倍体纯合子（haplotype homozygosity）来识别受选择的突变位点。下面就介绍最常见的EHH、iHH、iHS等概念。

extended haplotype homozygosity(EHH)，首先是有一个核心位点，其有两个等位基因，一个是祖系基因，一个是突变基因。这个时候我们可以把所有的单倍体分为两类，一类是含有祖系基因的单倍体（nA），另一类含有突变基因的单倍体（nD）。这个时候我们可以分别对着两类单倍体分别计算纯合度（FA和FD），然后将二者作比值（FD/FA），此时如果该突变位点受到选择，那么含有突变位点的单倍体的纯合度会升高，FD/FA也会增加。如下图：

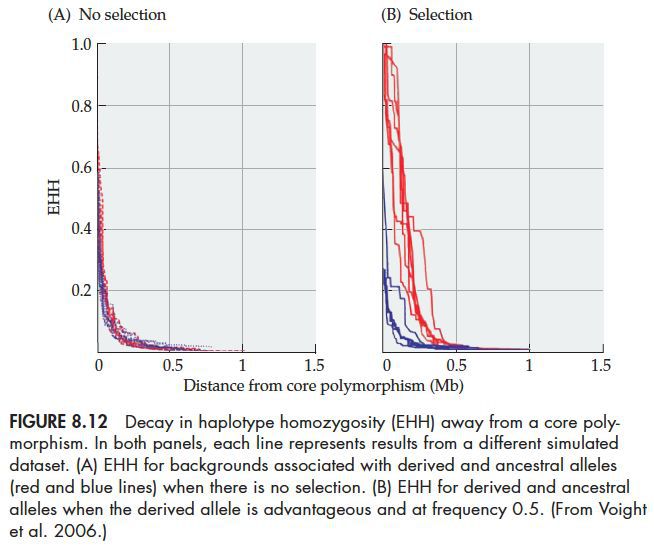
在没有选择的时候含有突变位点的单倍体（红色）和含有祖系基因的单倍体（蓝色）的EHH一样，而当突变位点受到选择时，会出现EHH升高。

那么有一个问题，在我们计算单倍体纯合度的时候选多大的窗口，一个极端的情况是，如果我们只用一个核心位点作为计算窗口，那么F=1，随着计算窗口的增加，F会逐渐减低（会有越来越多的重组事件提升窗口内的杂合度）。Voight(2006)提出了另一个相近的概念iHH(integrated haplotype homozygosity)，iHH综合了不同大小窗口计算EHH的结果。而实际上，iHH的计算结果就是上图中EHH曲线下的面积。同样地，为了判断iHH的大小，我们通常也会比较iHHA和iHHD，这就得到了另一个统计量，iHS（integrated haplotypescore）:

当有正向选择时，iHHD会比IHHA大，iHS因而会大于0.习惯上，我们还会对iHS进行标准化，即观测值减去均值，然后除以标准差。这时，标准化的iHS会分布在0左右，通常， iHS >2的时候我们会认为有正向选择的存在。不过，为什么这儿是绝对值？难道iHS<-2也会有正向选择吗？这主要是因为可能有重组的出现，会使得祖系基因重组到较高频率单倍体上，表现为含有祖系基因的单倍体在群体中频率很高，所以iHS<-2时，也认为有正向选择的存在。

另外，根据单倍体纯合度来识别正向选择的方法还有H12，即使用一个固定窗口中频率最高的两种单倍体的频数来衡量这个窗口中是否受到正向选择，不仅如此，它还能够区分开hard sweep和soft sweep，这时十分有用的。后面有机会会详细介绍。参考：

Garud, N. R., Messer, P.W., Buzbas, E. O., & Petrov, D. A. (2015). Recent selective sweeps in NorthAmerican Drosophila melanogaster show signatures of soft sweeps. PLoS genetics,11(2), e1005004.

最后，在使用连锁不平衡和单倍体频谱来识别自然选择的时候，一定要注意对结果的解释，因为不仅是自然选择，群体结构同样会产生和自然选择十分相似的结果！

（十三）单个群体种群史

https://zhuanlan.zhihu.com/p/360441864

种群的增长、缩小、分裂、融合等事件的发生都会在种群基因组多样性上留下印记。很多方法可以用来研究种群史，常用的参数有3个：有效群体数量 (Ne), 迁徙率 (m) 和种群分裂时间 (t)。

种群史在基因组上留下的印记很容易和自然选择留下的印记相混淆，所以在研究自然选择时，或者在研究种群史的时候，一定要弄清它们之间的相互影响。种群史既然是历史，我们的研究也只能是在宏观的层面对其研究，没有哪一个研究能够精确的给出一个种群的相关参数，绝大多数都是估计和假设。

单个种群的种群史

单个种群的种群史是最简单的一种情况，不会涉及迁徙率和种群分类合并的问题，只有一个Ne参数。种群事件也仅有Ne的增大或者Ne的减小。另外还有一种常说的“瓶颈”，即种群Ne先减小后增大。如下图：

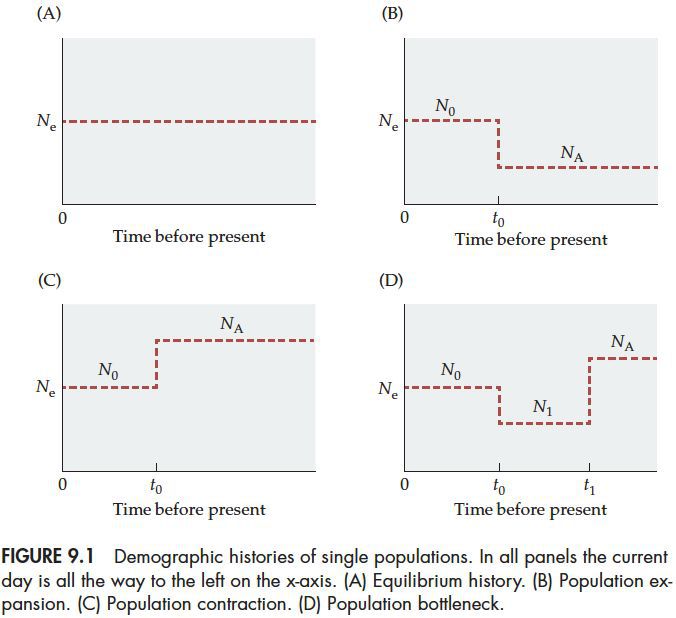
上图中涉及最开始的有效群体数量(NA)，当前有效群体数量Ne，以及事件t。需要指出的是，上图只是为了方便的简化模式，群体数量不会是突变，通常会以指数形式（r）增加或减小。描述一个瓶颈模型，通常用瓶颈效应强度，即种群的缩小程度（N1/NA），和瓶颈持续时间（t1-t0）。

种群大小变化对基因谱系的影响

两个个体能够溯祖到一起的速度取决于群体的数量。对于一个种群不变的二倍体群体，两个个体在一代中溯祖到一起的概率是1/2Ne.对于种群数量变动的个体，当种群数量比较大的时候，溯祖概率较低，种群小的时候溯祖概率较大。

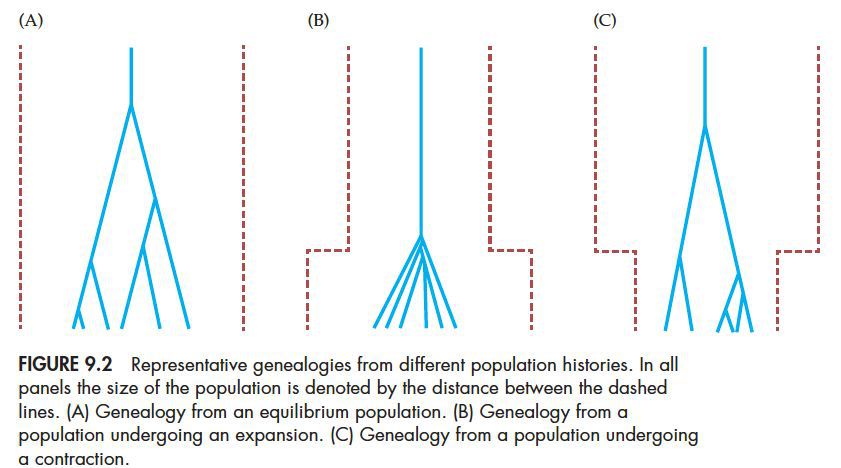
种群大小变化对基因频谱的影响

种群膨胀会导致一些描述等位基因频谱的统计量，如Tajima’s D, Fu and Li’s D，变成负值，种群中出现较多的低频等位基因。相反，种群收缩就导致这些统计量变成正值，种群中的低频等位基因被移除，中等频率等位基因相对增加。

对于瓶颈模型，种群大小变化对等位基因频谱的影响多种多样。取决于是收缩占主导优势还是膨胀占主导优势。如果膨胀占主导优势，则经过瓶颈事件之后，种群中会有过多的低频等位基因；反之，如果收缩占主导优势，那么种群中的中等频率等位基因会相对增多。如下图

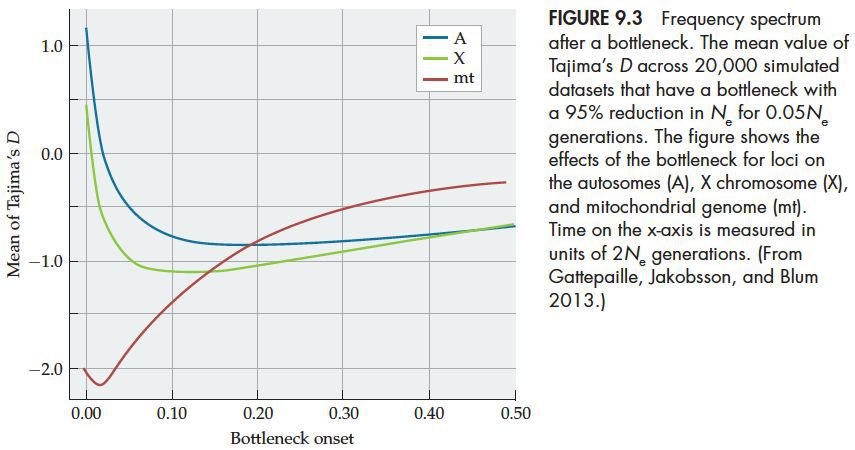
如果是近期发生的瓶颈事件，那么群体收缩会是主导力量，正常Tajima’s D为正值，如果是很久之前发生的瓶颈事件，那么当前群体受到种群膨胀的影响更大，这时种群中会有过多的低频等位基因，Tajima’s D为负值。

另外，上图中还分别表示了常染色体、X染色体和线粒体染色体的不同。这些染色体的有效群体数量是不同的，分别为2Ne, 1.5Ne和0.5Ne.即便这些小的群体数量的差异，它们所反映出受瓶颈效应的影响大小差别还是非常大的。尤其是其中的线粒体染色体，有效种群数量太小，以至于一个很近的瓶颈事件也会清除绝大多数旧变异，同时出现大量新的变异，主要呈现出种群膨胀的效果。

种群大小变化对其他变异参数的影响

对连锁不平衡（LD）的影响～群体的膨胀会有更多的机会带来新的变异，这些新的变异彼此不相关，导致LD水平变低；相反的，群体收缩会导致LD增高。

另外，在假设没有重组的情况下，可以根据谱系关系来推测各个阶段的有效群体数量，如下图：

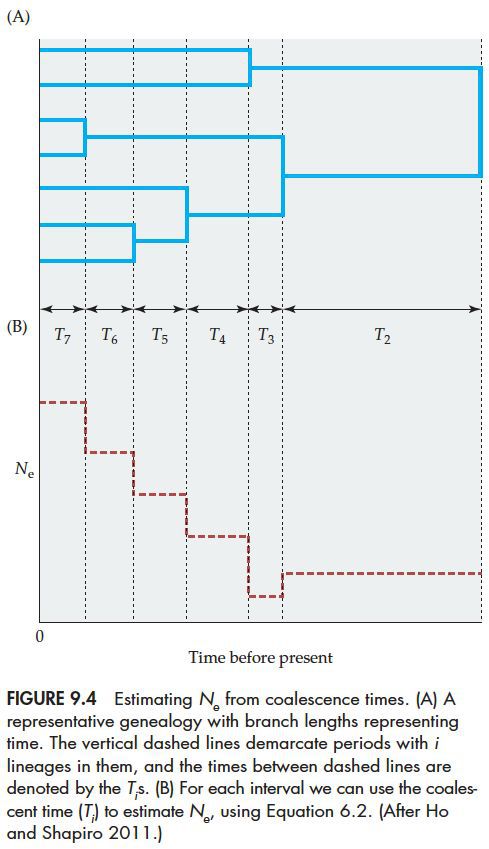
实际中，没有重组的假设很难得到满足，所以通常人们会选取很少重组的一段序列来建树推测有效群体数量变化。比如SMC（sequentially Markovian coalescent）方法就常用来推测不同时期群体数量的变化。

对IBD和IBS的影响～IBD（identical by descent）是指没有重组事件发生的一段共同序列的长度；IBS（identical by state）是指没有突变发生的一段共同序列的长度。

以IBS为例：

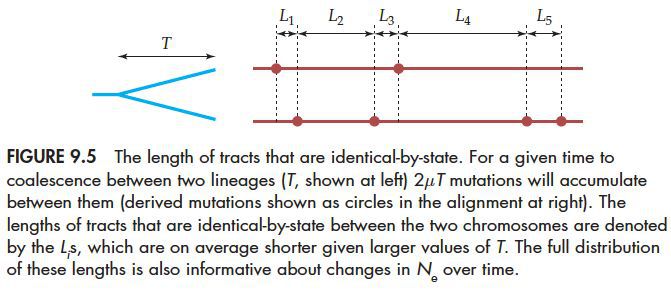
如果溯祖到一起的时间为T，那么在这两个分支上的突变累计数为2uT，所以T越大，累计突变越多，而对应的IBS（L1 - L5）也越短。如果我们把基因组中所有的IBS都考虑在内，就能够得到综合的T值情况，也进而能够推测Ne。

对于IBD也是同样的道理，综合考虑一个基因组中所有的IBD长度分布，能够推测Ne发小。

推测群体历史常用的方法

在没有自然选择的情况下，Ne的值能够大概代表群体大小的调和均数。在估计Ne的所有方法中，有3种数据类型。

第一种是SNP数据，假设SNP位点之间是相互独立的，对SNP的数据分析能够涵盖数千的样本量，比如Dadi ~根据扩散理论预测等位基因频谱，进而推测群体历史，Dadi既可以用于单一群体也可以用于多群体，能够估计不同时期各种不同的历史事件，另外还有stairway plot和fastNeutrino等工具。

第二种数据是短序列区块，通常为了简便，假设各个序列区块之间是完全随机重组，而区块内部没有重组，分析的样本量能够达到数百个个体。常用工具如skyline plot, BEAST。

第三种数据是一次分析全部基因组数据，通过全部基因组数据来推测Ne，但是这对计算量的要求很高，通常样本量也会很小，如pairwiseSMC模型，diCal, ARGweaver。

常用的方法就是似然估计和Bayesian方法。前者包括使用似然函数的full likelihood methods和使用模拟的approximate likelihood methods。但是随着计算机性能提高，后者的使用更加广泛，通过模拟一系列的参数组合，找到这符合我们观测结果的参数组合。当然，Bayesian的方法也使用的越来越多，如ABC（approximate Bayesian computation）。

（十四）多种群群体史

https://zhuanlan.zhihu.com/p/360442603

单个种群只涉及到Ne一个参数的变化，当多个种群存在时，还会涉及到种群分离时间（t）和种群之间的迁徙率（m）。如果当前有K个种群，那么就会有K-1个祖先，有K-1次分离。所以对于一个10个种群的大群体而言，整个种群结构模型中会有19（当下10 +祖先9）个Ne参数，9个时间t参数，同时会有162种迁徙率m参数。

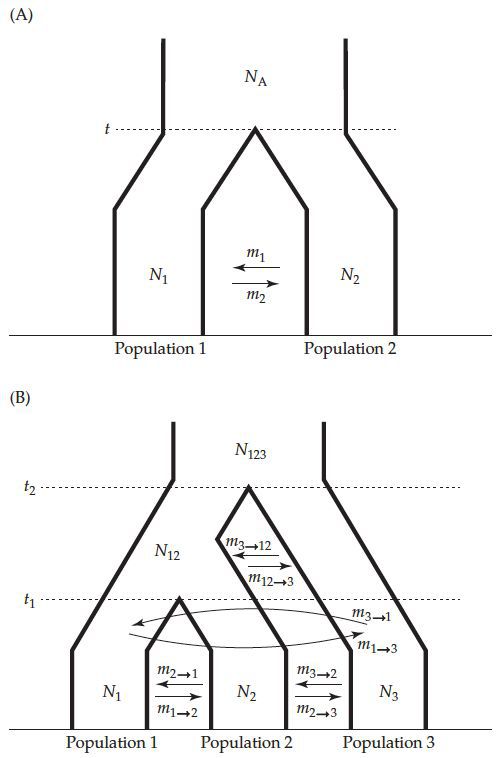
种群结构对等位基因频谱的影响

在没有基因流的情况下，种群之间的分化Fst与有效群体数量Ne和分化时间t有关，Ne越小，t越大，种群之间分化越大。而基因流会抵消一部分种群间的分化。

我们通常在采样时，并不知道种群结构，如果采样群体存在种群结构，即来自不同的群体，那么这种情况下就会对等位基因频谱产生影响。如果是两个很久之前就分离的群体，那么采样之后会出现过多的中等频率的等位基因，Tajima’s D会变成正值，这种基因频谱和平衡选择以及瓶颈事件产生的效果很相似。

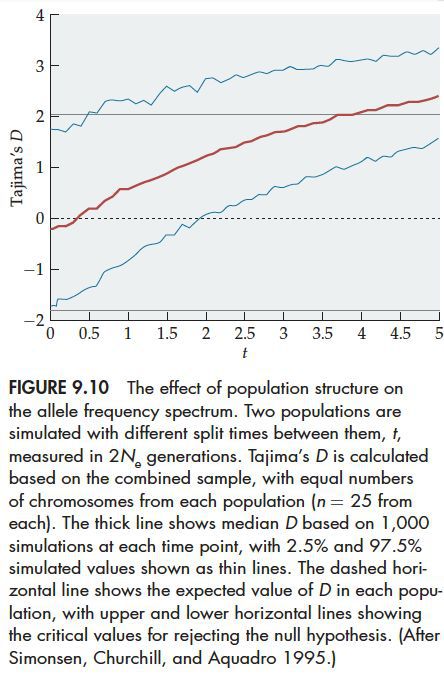
(随着两个群体的分离时间延长，采样群体中中等频率等位基因越来越多，Tajima’s D逐渐增高)

注意上面的情况是在两个群体中采同样的样本量，如果采得样本量不同，我们可能会有不同的等位基因频谱。一个极端的情况，我们采了50个群体，每个群体一个样本量，这个时候我们在等位基因频谱中可能观察到过多的低频等位基因，这就和定向选择或者群体膨胀很像了。种群之间的迁徙实际上会带来同样的效果，使我们认为的一个采样群体实际上是来自多个不同的群体。所以，我们在解释等位基因频谱的时候一定要小心，分清是否存在种群结构，是否有种群之间的迁徙。

多个种群群体史的推测

推测多个种群的群体史最常用的工具是Dadi，它能够处理很大的样本，但是每次只能处理最多3个群体。另一个工具是Jaatha，利用短序列区块数据，但是也只能处理2个群体。另外还有fastsimcoal2，能够处理多个群体。还有SMC++等工具。

种群关系网

admixture，它通常是指来自不同群体的个体合并在一起，形成一个新的群体。比如非裔美国人和拉丁裔美国人的融合。现在这个词越来越被泛用。不仅指两个不同群体的个体融合形成新的群体，也指一个群体向另一个群体中输入基因流。通常情况下，我们根据种群基因频率就可以构建一个种群关系网，常用的软件有TreeMix和MixMapper。

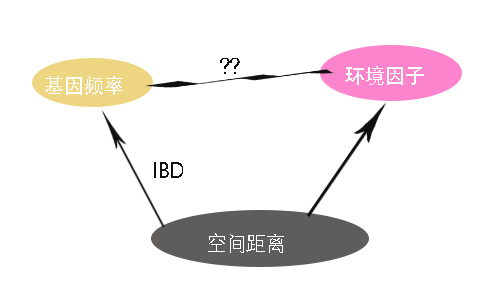
空间种群关系的分析

研究人员通过采集不同区域的群体样本来研究等位基因频率和环境因子的关系或者研究不同地理屏障对基因流的影响。它通常不会涉及多个物种，只会是一个物种的不同种群。

在研究空间种群关系中，有一个很重要的参数就是亲代和子代空间距离的方差，即扩散距离。如果群体间分化随空间距离增大而增大，那么这种现象也被称为isolation by distance(IBD, 注意和之前讨论的IBD – identical by descent不一样)。我们可以计算不同群体之间的Fst，然后将Fst/(1-Fst)作为纵坐标和空间距离作图，拟合回归模型，一次来判断群体之间是否存在IBD。IBD的存在意味着群体之间存在迁徙-漂变平衡的存在。回归模型的斜率取决于有效群体数量（或群体密度）和扩散距离的乘积。

当然研究种群的空间关系，更常用的是主成分分析（PCA），PCA起到降维的作用，例如使用PCA和空间插值，人们研究了欧洲人口的迁徙，根据第一主成分推测人口从东南向西北迁徙。

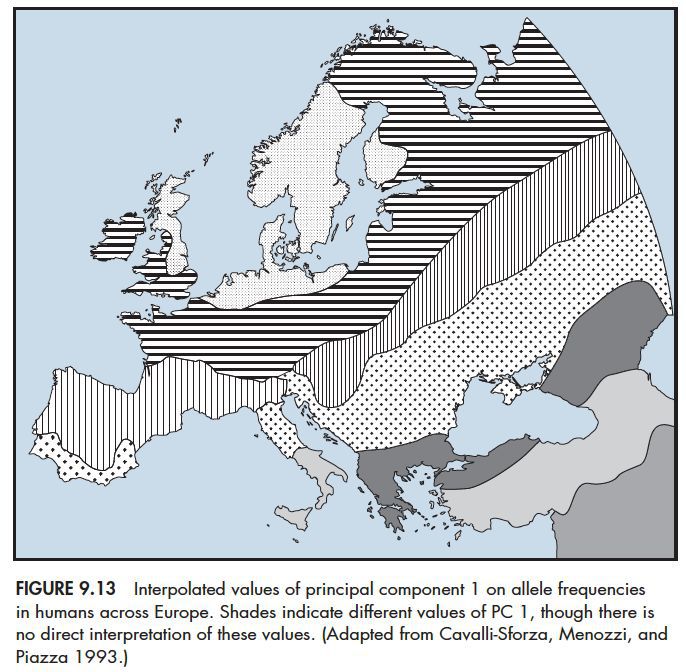
如果同时使用第一主成分和第二主成分作图，那么就可以很清楚的看清基因上和地理上的结构匹配程度。但是PCA并不适合推测种群扩散范围，PCA也不能反映出迁徙过程。同时PCA的准确性受到采样的影响。

除了PCA，还有两个常用的工具来推测空间种群关系，一个是EEMS，另一个是SpaceMix.前者能够直观的看出空间中种群迁徙的水平高低，也能够很好的找到阻碍基因流的屏障或者促进基因流的走廊。

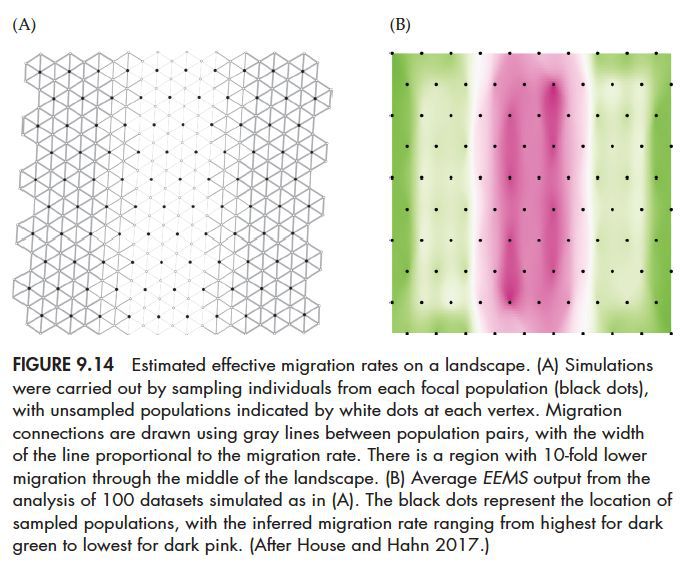
(红色区域表示低迁徙区，绿色部分表示高迁徙区)

SpaceMix能够清楚的推测基因流的方向和强度。

最后一种常见的研究是研究基因和环境的相关关系。和某个环境因子相关的基因很可能受到环境因子的选择。但是当存在IBD的时候，这种方法有一定的问题。空间上离得很近的群体，在基因上也会很相似，同时在环境因子上也很相似，也就是空间距离是研究基因和环境关系的一个混杂因素。所以会出现很多的假阳性结果。要想得到可靠的结果，就要控制空间距离这一混杂因素，幸运的事，有些软件已经能够做到这一点了，比如常用的Bayenv和LFMM。

（十五）群体史参数估计

https://zhuanlan.zhihu.com/p/360442715

之前讨论的数据都是多态性数据，如果不使用多态性数据，仅仅使用几个群体或者物种之间的序列信息，也可以用来研究群体遗传。

通过两个物种推测祖系参数

两个序列的分化通常要早于物种之间的分化。对于常染色体的位点，序列分化时间大概是在2NA代之前，NA是祖系有效群体数量。

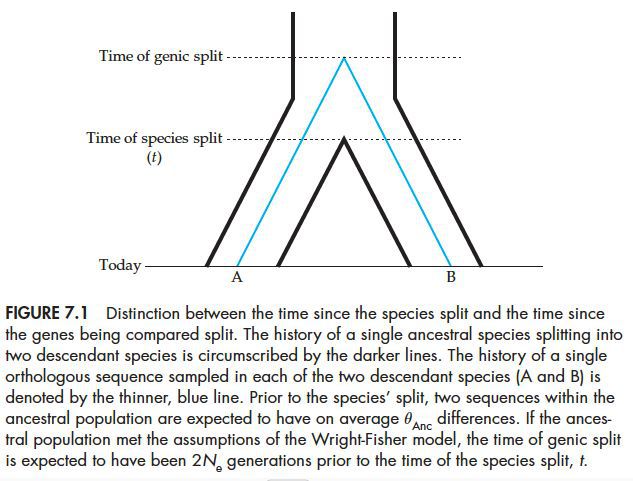
因此，可以以此来估计祖系的NA参数，但是这儿会有很多假设，比如各个位点的突变率相同，没有选择，没有迁徙，位点内部没有重组。如果这些条件不能满足，比如各个位点突变率不同，或者有迁徙，那么可能会导致苏族时间变成，NA参数估计偏大。

由一个基因或者位点来构建的演化树并不一定能够正确地反映出物种之间的演化关系。这种在基因水平和物种水平演化关系不一致的现象就是“不完全谱系分选”（incomplete lineage sorting，ILS）。

如下图A是三个物种的物种树：

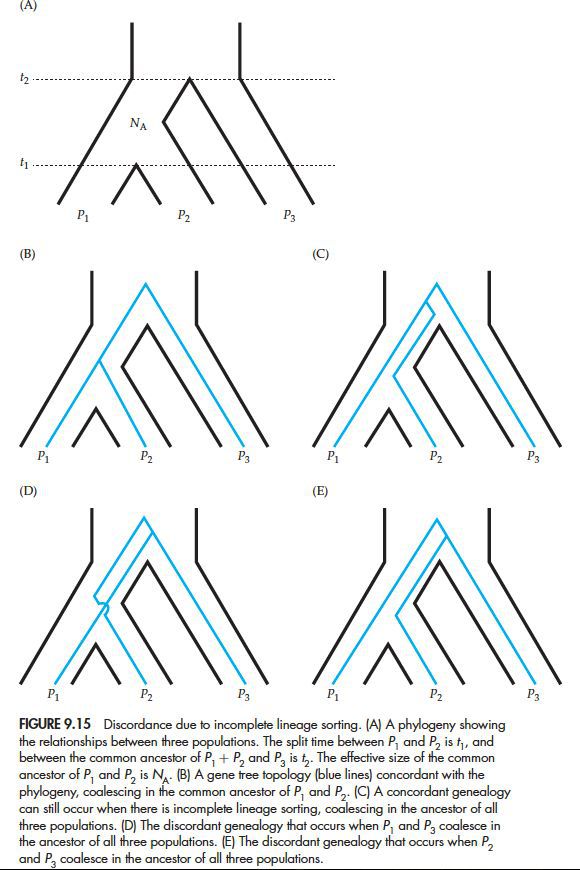
其中B的拓扑关系和物种关系一致，称之为“谱系分选”，其他的拓扑关系和物种关系不一致，即不完全谱系分选。ILS的概率有两个参数有关系，即NA和（t2-t1）。共同祖先的有效群体数量NA越大，谱系聚合时间越长，发生ILS的概率越小，时间（t2-t1）的时间越长，谱系聚合的概率越大，发生ILS的概率越大。注意上图中的C基因谱系关系和物种关系的拓扑结构一致，但是实质上也是ILS。同样的还要注意自然选择对上述情况的影响。

基因渗入

如下图：

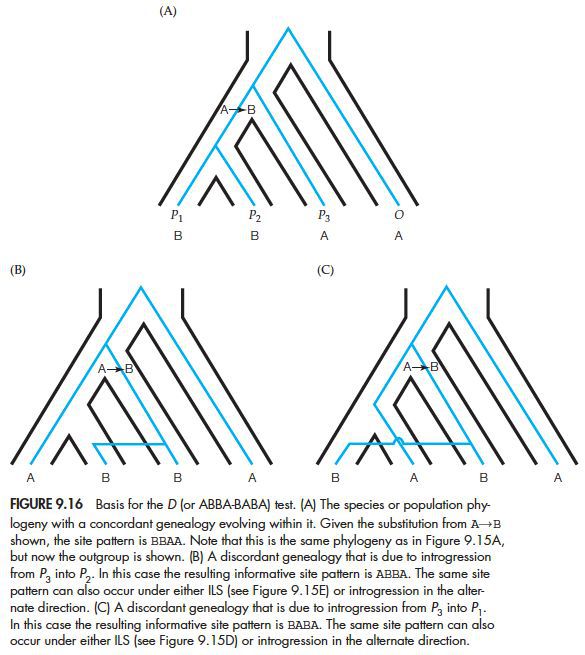
A图中在没有基因渗入的情况下，发生了一个突变A—> B，那么对应四种物种的基因变为BBAA，如果发生了P3—> P2的基因渗入，则会变为ABBA（B图），同样地如果发生P3—> P1的基因渗入，则变为BABA（C图）。所以有了一个新的统计量D，又称为ABBA-BABA检验或者Patterson’s D：

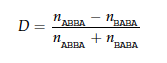
如果D > 0，说明有P2和P3之间的基因流，如果D < 0，说明有P1和P3之间基因流。D = 0，说明没有基因流或者P2-P3和P1-P3之间有相等的基因流。

推测群体史中要注意的问题

群体史的推测会受到自然选择和其他进化力量的影响。有效群体数量Ne也不应该简单的等效为群体个体数量的大小，Ne的变化可能是群体数量大小变化的结果，也可能是自然选择的影响。即便当下很多理论和方法来研究自然选择和群体史，但将它们的作用区分开来依然面临着困难。

如下图的模拟结果，在一个群体中实际群体数量是恒定不变的，但是估计出的有效群体数量Ne的数量受到定向选择的影响，发生很大的变化。

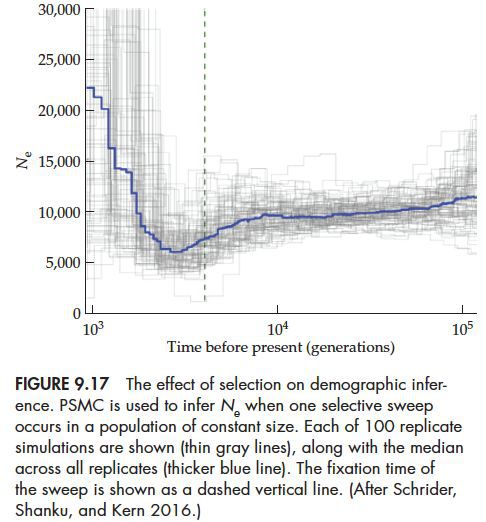
同样的道理，在研究迁徙的时候，参数m并不是指实际个体数量的迁徙，而是指有效的基因流渗入效应。另外，在我们研究群体史的时候，很多参数都是估计的，而且他们之间关系密切，一个参数的估计偏差过大会严重影响另一个参数估计的准确性。所以，应该避免在参数估计过程中某一个参数的权重过高。

（十六）群体基因组

https://zhuanlan.zhihu.com/p/360442785

随着测序技术的进步，人们对群体的遗传学研究不仅局限在某个基因位点，而是迅速扩展到全基因组。以果蝇为例，从对一个位点的研究（1983年），到两个位点研究（1986年），到20个位点（1992），到105个位点（2003）再到全部位点（2007年之后）。当然，对全基因组的研究并不是简单的将对位点研究堆积起来，而是在一个更大尺度，当高水平上全面的了解选择和进化。

在基因组水平对自然选择的识别

目前已经有很多研究通过对全基因组水平的扫描，来识别受选择的区域和位点。比如常发现与免疫相关、与病原应答相关的很多基因受到正向选择，与MHC相关的基因受到平衡选择。通过全基因组扫描识别选择目标，进而推测什么样的表型适应什么样的环境。当然，通过基因组所描识别出的受选择的基因和推测的表型，只是为我们提供了一个方向，更确定的结果还需要实验数据的支持。

对于群体遗传学研究者来说，比较关注的是哪种自然选择以及以多大的频率作用在基因组上。比如，正向选择导致碱基替代率的情况，平衡选择导致的氨基酸多态性的比例。再如，选择开始时，受选择位点在群体中多样性情况，是一个新突变还是既有的多态性位点？是直接受到选择的目标，还是因为LD造成的关联选择？这些问题都是群体基因组研究要回答的问题。

自然选择VS群体史

在群体遗传学研究中，说过很多次的一个问题是区分自然选择和群体史。不过有些方法在识别自然选择时，不受群体史的影响，比如通过比较同义突变和非同义突变来识别自然选择的方法，它能够避免群体史对结果的干扰。

而另外很多的方法，通过关联选择来比较观测结果和理论结果的差异来识别自然选择的方法（比如等位基因频谱）通常对群体史非常敏感。使用LD来识别自然选择的方法同样受到群体史的影响。

很对人会认为自然选择对基因组的影响是局部的，而群体史会影响到整个基因组，可以以此来区别自然选择和群体史。但是这种方法存在一些问题，并不是所有的选择作用都是局部的效应，如果选择作用遍布整个基因组（比如在很多真核生物中），那么基因组表现出来的就不是群体史的效应，而是选择的作用。

识别选择目标的通用方法

全基因组扫描通常是根据关联选择来识别受选择的基因区域，而具体哪一个突变位点受到选择并不得而知。如果受关联选择的区域越大，我们找到具体位点的难度也就越大。我们常用的方法有两种，一种是基于模型的，另一种是根据异常值。

基于模型的方法是要事先知道群体史，或者通过能够模拟一系列可能的群体史，然后根据群体史来判断一个位点出现观测值的概率大小（即P值）。

这儿就涉及到一个基因组学中最常见和难以避免的问题，即P的多重比较。通常情况下，对于一次比较，我们会认为P<0.05即可以拒绝无效假设。但是当我们进行了很多次检验的时候，如果仍然按照P<0.05的标准来拒绝无效假设就会出现很多假阳性。如下图A：

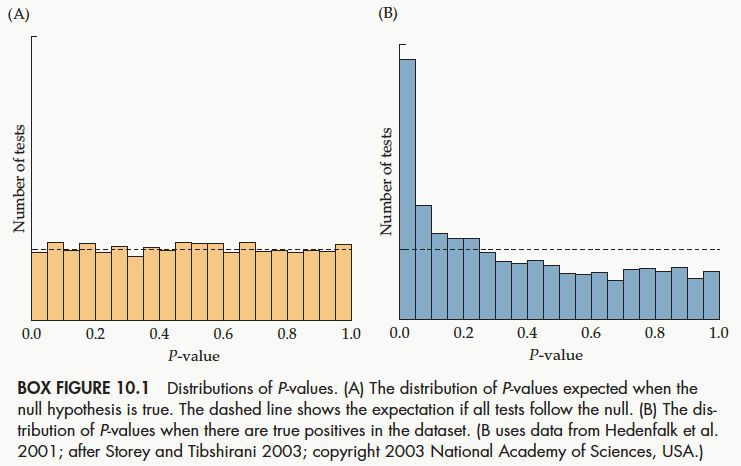
在无效假设的情况下，P值在0-1之间均匀分布，按照0.05的标准，进行1000次检验，我们会得到50次的假阳性。所以要调整P值。通常用Bonferroni的P值校正方法，根据假设检验的次数来校正，但是这种方法有时候过于保守，很多真阳性的结果也被剔除掉了。所以有了另一种方法FDR校正。比如在上图B中，进行1000次检验，观测到200次P< 0.01，而在无效假设成立的条件下，仅仅能够观测到10次P<0.01，所以这个时候在200次观测结果中，可能有10次史假阳性，所以FDR = 10/200 =0.05.通常在研究中FDR取0.05，有些研究也会渠道0.2或者0.3。

基于模型的方法有一个假设，就是选择在基因组中不是广泛存在，而基因组信号值的平均水平反应的是种群史（如Tajima’s D）。而如果这种假设不成立，即在基因组中存在很多选择和关联选择，基因组信号值的平均水平已经显著受到了选择的影响，这个时候就会出现很多假阴性，很多选择信号会被误认为是群体史造成的。

另一种基因异常值来识别选择信号的方法通常不会受到群体史影响（虽然它的假设也是选择在基因组中不是广泛存在的）。异常值的判断通常根据经验，比如前1%认为是异常值。通过异常值来判断选择位点通常用于群体史未知，或者群体史过于复杂难以模拟的情况。但是它的缺点也是显而易见的，即便群体中没有选择，那么1%的判断就会带来1%的假阳性率。反之，如果群体中存在大量的选择，1%的判断又会带来很多假阴性。所以使用的时候需谨慎。

进行全基因组扫描识别自然选择的方法

一个群体中的样本

通常不涉及种群分化情况，比如Tajima’s D、类D的参数和基于单倍体纯合子的方法。如果有选择的存在，这类方法通常在基因组上表现为一个低谷。

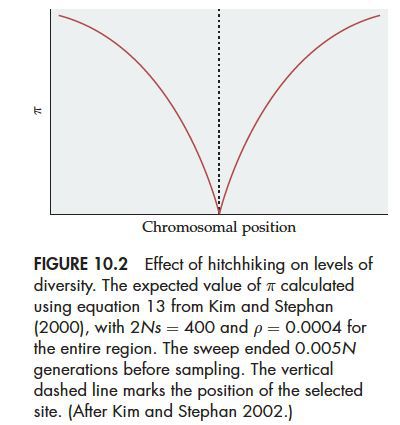
即由于LD的存在，在受选择位点周围出现核苷酸多样性降低，随着远离受选择位点，降低程度减少，形成低谷。低谷的大小和s/c成比例，选择系数越大，重组水平越低，低谷越大。等位基因频谱表现为，受选择位点周围出现大量低频等位基因，而紧靠选择位点的区域出现大量高频等位基因。

常见的方法有CLRT (composite likelihood ratiotest), SweepFinder，SweeD，iHS等。有两个关键的因素决定能够正确的识别受选择位点，一个是距离选择结束的时间，距离结束时间越短，信号越明显，识别率越高；反之，时间越长，信号消磨殆尽，识别越困难。第二个是群体史，非平衡状态的群体会带入很多混杂信号（如群体膨胀或者群体瓶颈事件），识别选择受到干扰。

多个群体样本

如果是有来自多个群体的样本，那么通常基于两种方法来识别群体中的选择：等位基因频率的不同和多样性水平的比较。

比如Fst用来比较种群之间等位基因频率差异，以此来识别选择位点。

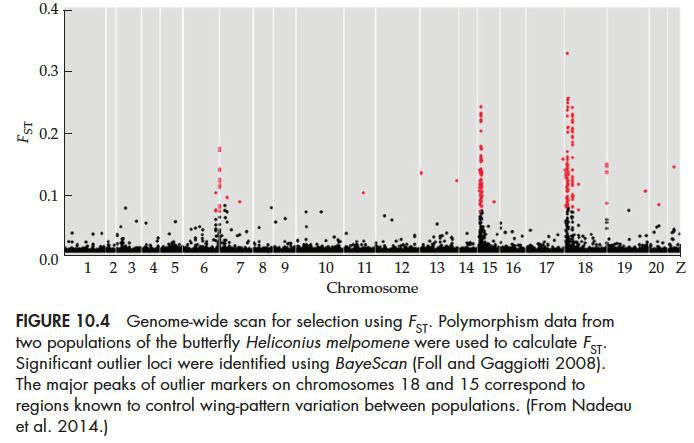
再如使用π来比较不同种群核苷酸多样性水平。

全基因组扫描中非独立性的问题

非独立性来源于两个方面，一个是生物学非独立性，另一个是方法学上的非独立性。比如在方法上常用扫描窗口的方法，相邻窗口之间往往会有一定比例的重叠（步长<窗口），这就会低估扫描参数的标准误差。另一种非独立性就是当我们使用多种方法的时候，他们之间并不一定完全不同，比如Tajima’s D和Fst，它们都受到多样性π的影响，所以如果一个位点被Tajima’s D和Fst支持是受到选择，那么也并不能说这种选择得到了两种独立方法的证明。这种错误在很多研究中经常遇到。

另外，相邻的位点之间往往有相似的系统发生史和相似的突变率。所以相邻位点之间的多样性、分化水平、等位基因谱等也很相似。所以在一个基因区域的选择信号，我们很难分别出是一个事件造成的，还是有多个事件作用的结果。

（十七）分子群体遗传学的未来方向

https://zhuanlan.zhihu.com/p/360442937

作为本系列的最后一部分，将讨论一下分子群体遗传未来的发展方向。随着计算机新能的提高和测序技术的进步，分子群体遗传在未来也会变得愈加重要，甚至会出现一些我们当前无法预测的应用。

机器学习在群体遗传学中的应用

机器学习是当前热点领域，通过计算机科学和统计学的整合在凌乱的数据中发现规律。而分子遗传学就是一门与大数据打交道的学科，因而机器学习在分子群体遗传中也应该有重要应用。我们之前学过很多群体遗传参数，如有效群体数量、突变率、重组率等等，我们通过机器学习更好的预测群体遗传参数。

机器学习分为有监督的机器学习（supervised machine learning）和无监督的机器学习（unsupervised machine learning）。有监督的机器学习是事先给训练集加上标签，然后根据这些标签去训练参数（“练参”）。无监督的机器学习则没有事先在训练集上添加标签，完全靠机器自己去对数据进行分类，提取最优参数。

在分子群体遗传中，有监督的学习中用到的训练集通常是在一系列参数已知的条件下通过计算机模拟得到的。通过训练集的训练得到一个分类器，并以此对未知数据进行分类。比如使用有监督的机器学习来识别正向选择以及是哪一种形式的正向选择。最近通过神经网络来实现的深度学习在分子遗传中也有应用。

无监督机器学习在分子群体遗传中最代表性的应用就是隐形马可夫模型（HMM），能够将基因组自动分成不同的区域，如根据GC含量不同，将基因组分段；推测染色体不同区域的祖先；研究不同种群间染色体高或低基因流区域；识别sweep影响的范围；确定选择在基因组上的作用区域；研究群体史等。

古DNA研究

测序技术的进步带来的另一有意思的领域就是古DNA。由于古DNA的降解和大量细菌遗传物质的污染，使得早期的研究多是使用线粒体或者叶绿体基因组。二代测序技术则使得研究者能够很便宜的得到大量的核基因组序列。

最早的大范围对古DNA研究包括了对4万年前洞熊的研究，以及对猛犸象、尼安德特人的研究。很快，全基因的测序被应用到了古人类、尼安德特人和丹尼索亚人。现在已经有数百个古人类基因组了。

全组装基因组群体

目前短阅读片段测序都是要和参考基因组比对组装，所以位于参考基因组以外的序列无法获得；或者是参考基因组和待组装基因组分化很大的区域，也无法进行很好的组装。另外对于拷贝数变异和高度重复序列，已很难准确的进行比对。这些问题都当前的研究带来很多麻烦。

所以新的测序技术，特别是长阅读片段测序（又称为“第三代测序”）为这些问题的解决带来了希望。它能够得到数十kb的读长，比如PacBio和Nanopore的测序技术。

全组装基因组不仅要求更高的测序技术，也给计算分析带来了挑战。比如参考基因组能够提供给研究者基因位置和基因注释，但如果我们得到的是一个全组装基因组，其中一部分能够比对到参考基因组上，但是另外一部分却无法在参考基因组上找到位置！这就成了一个很麻烦的问题。目前有些研究的做法是在基因分化程度高的区域（如人的MHC区域）加入“备选”（alternate）参考基因组，一次来避免有些区域无法比对的问题。还有的解决方法是不用参考基因组，而是以自己的全组装基因组作为参考，并根据新加入的基因组随时修改补充自定义的参考基因组。但其中的问题是，每次添加都会改变自定义参考基因组坐标，非常麻烦；而且全基因组比对是很耗费计算力的，短测序尽可能的避免了这个问题，但是全组装基因的长测序以及全基因组比对，又将比对计算复杂化了。

深度群体测序

测序价格的降低也使得测序深度增加有了可能。比如人类的基因组测序深度从1000个基因组（2012年）很快增加到10000个（2016年），而人类外显子组的测序从2400个个体（2012年）迅速增加到60000个（2016年）。深度测序能够发现稀有变异类型，以及最近的群体史。目前深度测序最常用的是推测突变率和突变类型，很低频率的变异很可能还没有受到自然选择的作用，因为通过研究它们能够使我们直观的了解群体中的突变情况。

对着测序深度的增加，测序个体数增加，这个个体之间的关系也必须是我们考虑的一个问题。样本个体数很少时，它们之间的血缘关系可以忽略，但是样本量的增加，很有可能他们之间存在较近的血缘关系。