liuyujie0136's Website

A website for self learning, collecting and sharing.
Volcano Plot 火山图简介
火山图是散点图的一种,它将统计测试中的统计显著性量度(如p-value)和变化幅度相结合,从而能够帮助快速直观地识别那些变化幅度较大且具有统计学意义的数据点(基因等)。常应用于转录组研究,也能应用于基因组,蛋白质组,代谢组等统计数据。
所以关于火山图,要先理解每个点是什么(点代表基因、样品、通路或其它的,这个认识可以来自于常识,更准确的是看作者的描述),然后看横轴代表什么、纵轴代表什么,再看图例中展示的其他信息,如颜色、大小和形状分别代表什么。这些都理顺了,图理解就不难了。
火山图的基本理解
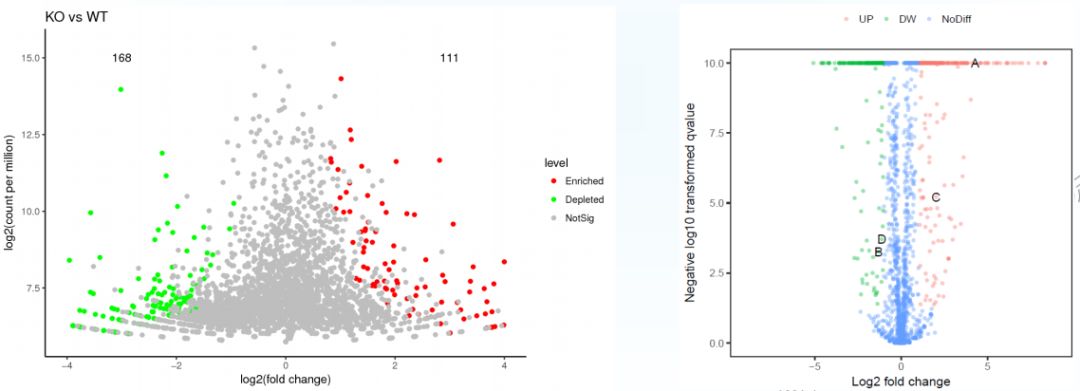
如图一:
- 每个点代表一个检测到的基因。
- 横轴和纵轴用于固定点在空间的位置。
- 一般横轴是
Log2(fold change),点越偏离中心,表示差异倍数越大。 - 纵轴是
-Log 10 (adjusted P-value),点越靠图的顶部表示差异越显著。 - 点的大小和颜色也可以表示更多的属性,如下图中点的颜色标记其对应的基因是上调, 下调还是无差异。大小也可用于展示基因表达的平均丰度,一般我们关注表达水平较高且差异较大的基因用于后续的分析和验证。
火山图理解常见的几个问题
-
什么是
fold change? 翻译成中文是差异倍数,简单来说就是基因在一组样品中的表达值的均值除以其在另一组样品中的表达值的均值。所以火山图只适合展示两组样品之间的比较。 -
为什么要做
Log 2转换? 两个数相除获得的结果(fold change)要么大于1,要么小于1,要么等于1。对于基因差异,简单说,大于1表示上调(可以描述为上调多少倍),小于1表示下调(可以描述为下调为原来的多少分之多少)。大于1可以到多大呢?多大都有可能。小于1可以到多小呢?最小到0。用原始的fold change描述上调方便,描述下调不方便。绘制到图中时,上调占的空间多,下调占的空间少,展示起来不方便。所以一般会做Log 2转换。默认我们都会用两倍差异 (fold change == 2 | 0.5)做为一个筛选标准。Log 2转换的优势就体现出来了,上调的基因转换后Log 2 (fold change)都大于等于1,下调的基因转换后Log 2 (fold change)都小于等于-1。无论是展示还是描述是不是都更方便了。 -
什么是
adjusted P-value? 这里面就涉及到一个统计学问题了。做差异基因检测时,要对成千上万的基因分别做差异统计检验。统计学家认为做这么多次的检验,本身就会引入假阳性结果,需要做一个多重假设检验校正。这个校正怎么做呢?最简单粗暴的方法是每一次统计检验获得的P-value都乘以总的统计检验的次数获得adjusted P-value(这就是Bonferroni correction)。但这样操作太严苛了,很容易降低统计检出力,找不到有差异的基因。后续又有统计学家提出相对不这么严苛的计算方法,如holm, hochberg, hommel, BH, BY, fdr等。BH是我们比较常用的一个校正方法,获得的值是假阳性率FDR(false discovery rate)。FDR筛选时就可以不用遵循0.05这个标准了。我们可以设置FDR<0.05表示我们容许数据中存在至多5%假阳性率;FDR<0.1表示我们对假阳性率的容忍度至多是10%。当然如果说我们设置FDR<0.5,即数据中最多可能有一半是假阳性就说不过去了。 -
同样为什么做
-Log 10转换呢? 因为FDR值是0-1之间,数值越小越是统计显著,也越是我们关注的。-Log 10 (adjusted P-value)转换后正好是反了多来,数值越大越显著,而且以10为底很容易换算回去。
再看火山图
- 整体来看,基因有上调就有下调,图整体是以
X=0的垂线左右对称的。如果数据中大部分点都是上调或下调,成偏态分布时,需考虑标准化步骤没有处理好,或数据存在批次效应,导致数据存在系统偏差。 - 图的左上角和右上角是差异基因集中的地方,也是我们关注的重点。
- 图一中左侧的火山图还展示了基因表达的平均丰度,即基因在所有样品中表达的均值。一般变化倍数大、平均表达也比较高的基因会更可信,更适合后期实验检测,否则就算变化倍数再大,表达低的基因也难以被检测到。